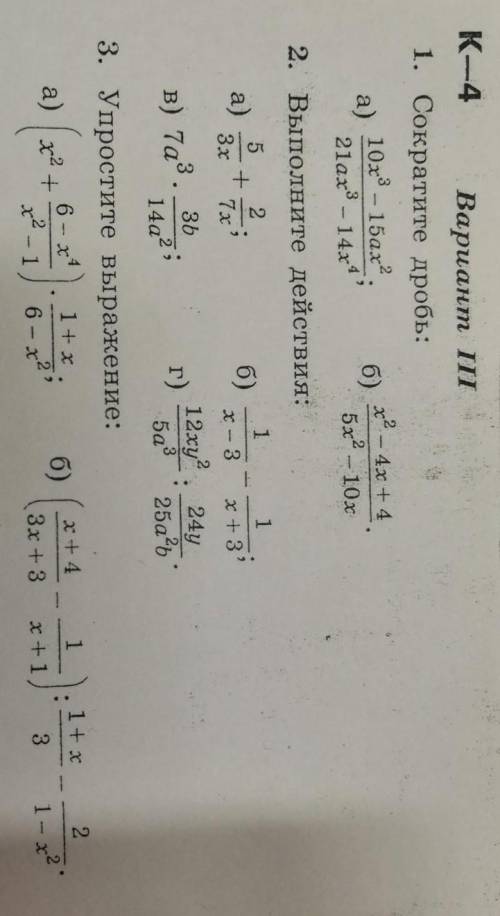
ответы:
Снизу
Объяснение:
1.а) 5x²(2x-3a)/7x(3a-2x)=5x(2x-3a)/-7(2x-3a)=5x/7
б) (x-2)²/5x(x-2)=x-2/5x
2. а) (35+6)/21x=41/21x
б) x+3/(x-3)(x+3)-(x-3)/(x-3)(x+3)=6/x²-9
в) 7a³*3b/14a²=3ab/2=1,5ab
г) 12xy²/5a³ * 25a²b/24y=xy*5b/2a=5xyb/2a
3. а) 1. x²+6-x⁴/x²-1=(x²(x²-1)+6-x⁴) x²-1=-x²+6/x²-1=6-x²/x²-1
2. 6-x²/(x-1)(x+1) * 1+x/6-x=1/x-1
б) 1. x+4/3(x+1)-3/3(x+1)=x+1/3(x+1)=1/3
2. 1/3*3/1+x=1/1+x
3. 1/1+x-2/(1-x)(1+x)=1-x/x²-1 - 2/x²-1= -x-1/x²-1=x+1/1-x²=1+x/(1-x)(1+x)=1/1-x
Объяснение:
Во-первых, область определения
-x^2 - 8x - 7 >= 0
x^2 + 8x + 7 <= 0
(x + 1)(x + 7) <= 0
x = [-7; -1]
Во-вторых, выделяем корень
√(-x^2 - 8x - 7) = -ax + 2a + 3
Возводим в квадрат
-x^2-8x-7 = (-ax+2a+3)^2 = a^2*x^2-4a^2*x+4a^2-6ax+12a+9
x^2*(a^2 + 1) + x*(8 - 4a^2 - 6a) + (7 + 4a^2 + 12a + 9) = 0
x^2*(a^2 + 1) + 2x*(-2a^2 - 3a + 4) + (4a^2 + 12a + 16) = 0
Получили квадратное уравнение.
Если оно имеет только 1 корень, то D = 0
D/4 = (-2a^2 - 3a + 4)^2 - (a^2 + 1)(4a^2 + 12a + 16) =
= (4a^4 + 12a^3 + 9a^2 - 16a^2 - 24a + 16) -
- (4a^4 + 4a^2 + 12a^3 + 12a + 16a^2 + 16) =
= 9a^2 - 16a^2 - 24a - 4a^2 - 12a - 16a^2 = -27a^2 - 36a = -9a(3a + 4) = 0
a1 = 0; a2 = -4/3
Подставляем эти а и проверяем х.
1) a = 0
0 + √(-x^2 - 8x - 7) = 3
-x^2 - 8x - 7 = 9
-x^2 - 8x - 16 = -(x + 4)^2 = 0
x1 = x2 = -4
2) a = -4/3
-4x/3 + √(-x^2 - 8x - 7) = -8/3 + 3 = 1/3
√(-x^2 - 8x - 7) = 4x/3 + 1/3 = (4x + 1)/3
9(-x^2 - 8x - 7) = (4x + 1)^2
-9x^2 - 72x - 63 = 16x^2 + 8x + 1
25x^2 + 80x + 64 = (5x + 8)^2 = 0
x1 = x2 = -8/5
5040
Объяснение:
Чтобы решить эту задачу, нужно использовать теорию вероятности.
У нас есть 7 разрядов, куда будут подставляться цифры (число 5720198 - семиразрядное) и 7 вариантов цифр для каждого разряда (5,7,2,0,1,9,8). Кроме того мы знаем, что цифры будут перестанавливаться, а значит каждый из вариантов цифр может появляться в примере только один раз. Все готово для решения.
В первом разряде может присутствовать любой из семи вариантов:
7
Во втором - на один меньше, так как один из вариантов уже присутствует в перовом разряде.
7*6
В третьем - еще на один меньше по той же причине
7*6*5
В итоге получаем следующий пример:
7*6*5*4*3*2*1 = 5040
В краткой форме это будет выглядеть так:
7!=5040
ответ: 5040 вариантов
На фото
Объяснение: