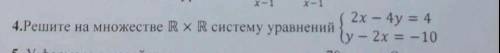
Объяснение:
№1
Примем за х количество гвоздей по 3 рубля,за у-количество гвоздей по 4 рубля.Тогда х+у=20,3х+4у=72.Решим систему уравнений:
х+у=20
3х+4у=72
х=20-у
3(20-у)+4у=72
60-3у+4у=72
у=72-60
у=12 -гвоздей по 4 рубля
х=20-12
х=8 гвоздей по 3 рубля
№2
10-4(2х-у)+10х=5(3+у)
3х+у-5=2(3-2х)-2у
10-8х+4у+10х=15+5у
3х+у-5=6-4х-2у
2х+4у-5у=15-10
3х+у+4х+2у=6+5
2х-у=5 *3
7х+3у=11
6х-3у=15
7х+3у=11
13х=26
х=26:13
х=2
2*2-у=5
у=4-5
у= -1
ответ(2;-1)
№3
-6х+5у=9 *3
18х-15у=27
-18х+15у=27
18х-15у=27
0 не равно 54,поэтому система решения не имеет.
Натуральные числа - это числа, используемые при счете, т.е. 1, 2, 3, 4,...
Целые числа - это натуральные, им противоположные и число 0, т.е.
... -3, -2, -1, 0, 1, 2, 3, ...
Рациональные числа - это целые числа и дроби (как положительные, так и отрицательные), поэтому рациональное число всегда можно представить в виде отношения m/n, где m - целое, а n - натуральное числа.
Например, 1/2, 2 целых 3/7, -5 целых 1/9, 0,089 и -2 = -4/2 = -100/50 и др.
Таким образом, любое рациональное число можно записать в виде бесконечной периодической десяичной дроби, например, 2/3 = 0,666... = 0,(6).
Иррациональные числа - эо все числа, которые нельзя представить в виде бесконечной периодической десятичной дроби, а только в виде непериодической десяичной дроби.
Например, √2 = 1,4142..., π = 3,14159265358... и др.
Поэтому число 0 - рациональное.