Пусть 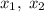 — решения уравнения
— решения уравнения 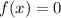 . По условию
. По условию 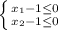 . Можно сделать замену:
. Можно сделать замену: 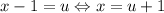 и рассмотреть функцию
и рассмотреть функцию 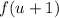 . Переформулируем условие: найти все значения параметра
. Переформулируем условие: найти все значения параметра  , при каждом из которых уравнение
, при каждом из которых уравнение 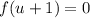 имеет два различных неположительных решения.
имеет два различных неположительных решения.
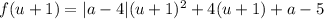 , после преобразований получим
, после преобразований получим 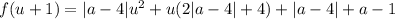 . Необходимым и достаточным условием неположительности решений явлется неположительность суммы и неотрицательность произведения корней. Применяя теорему Виета, переходим к системе:
. Необходимым и достаточным условием неположительности решений явлется неположительность суммы и неотрицательность произведения корней. Применяя теорему Виета, переходим к системе:  . Сразу заметим, что
. Сразу заметим, что 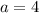 не подходит, так как дает уравнение с не более чем одним решением. Система эквивалентна следующей:
не подходит, так как дает уравнение с не более чем одним решением. Система эквивалентна следующей: 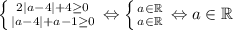 (1)
(1)
Теперь нужно наличие двух различных решений. Здесь удобно вернутся к изначальному уравнению (так как мы просто двигали параболу горизонтально). 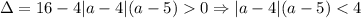 , это неравенство эквивалентно системе:
, это неравенство эквивалентно системе: 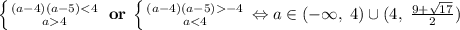 (2).
(2).
Пересекая (1) с (2) получим ответ.
ответ: 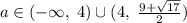
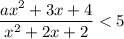
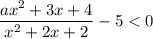
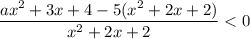
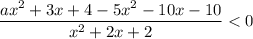
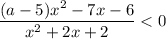
Неравенство вида 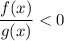 равносильно двум системам неравенств:
равносильно двум системам неравенств:
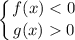 и
и 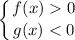
Тогда имеем две системы неравенств:
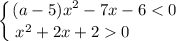 и
и 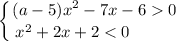
Рассмотрим первую систему неравенств:
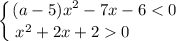
Решим второе неравенство системы:
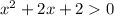
Пересечение с осью абсцисс:
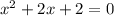
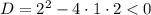
Дискриминант отрицательный, значит график квадратичной функции 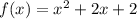 находится над осью абсцисс и при любых
находится над осью абсцисс и при любых  больше нуля.
больше нуля.
Тогда решением неравенства будет 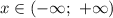
Рассмотрим первое неравенство системы:
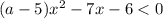
Поскольку следует найти значения параметра  , при которых
, при которых 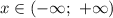 , то для решения системы неравенств нужно, чтобы и данное неравенство имело решение
, то для решения системы неравенств нужно, чтобы и данное неравенство имело решение 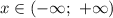
Если 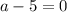 , то есть
, то есть 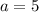 , то имеем линейное неравенство:
, то имеем линейное неравенство:

Решением данного неравенства будет 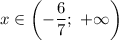 , что не удовлетворяет условию задачи.
, что не удовлетворяет условию задачи.
Тогда при 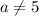 решим неравенство.
решим неравенство.
Если 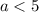 , то имеем параболу с ветвями, направленными вниз, если
, то имеем параболу с ветвями, направленными вниз, если 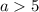 , то имеем параболу с ветвями, направленными вверх.
, то имеем параболу с ветвями, направленными вверх.
Пересечение с осью абсцисс:
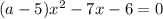
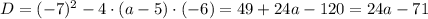
Если 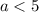 , то данное неравенство будет иметь решение
, то данное неравенство будет иметь решение 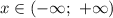 , если
, если 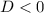 , то есть если
, то есть если  или
или 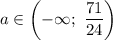
Если 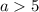 , то данное неравенство не может иметь решение
, то данное неравенство не может иметь решение 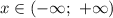
Таким образом, если 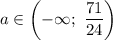 имеем решение
имеем решение 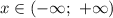
Рассмотрим вторую систему неравенств:
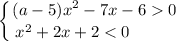
Решим второе неравенство системы:
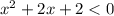
Пересечение с осью абсцисс:
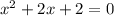
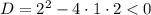
Если дискриминант отрицательный, то квадратичная функция 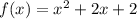 никогда не будет меньше нуля.
никогда не будет меньше нуля.
Тогда решением неравенства будет 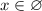
Тогда общим решением системы неравенств будет 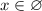 , независимо от значений параметра
, независимо от значений параметра 
ответ: 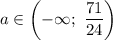
30 градусов
Объяснение: