Перед тем как выражать , нужно рассмотреть случаи, когда дробь положительная, а когда отрицательная:
Если такая дробь положительная, то при нахождении переменной знак неравенства меняться не будет (так как делим (умножаем) на положительное число):
Решим неравенство методом интервалов.
а) ОДЗ:
б) Нуль неравенства:
в) Решением данного неравенства будет .
При таких значениях параметра знак неравенства меняться не будет:
Если такая дробь отрицательная, то при нахождении переменной знак неравенства измениться на противоположный (так как делим (умножаем) на отрицательное число):
Решим неравенство методом интервалов. Решением данного неравенства будет .
При таких значениях параметра знак неравенства изменится:
ответ: если , то ; если , то ; если и , то неравенство не имеет решений.
3. Данная система неравенств решается в зависимости от значений параметра , поэтому:
1) Рассмотрим случай, когда решение неравенств пересекается:
Если , то есть , то в объединении с получаем при Если , то есть , то в объединении с получаем, что таких не существует, то есть такого варианта эта система не имеет.
2) Рассмотрим случай, когда решение неравенств не пересекается (когда система не имеет решений):
Оставшийся промежуток является решением этого варианта:
ответ: если , то ; если , то ; если , то система не имеет решений.
Можно использовать метод док-ва от противного, предположив, что b > a или что b-a=c>0. b = c+a b^2=c^2+2ac+a^2 a^2-b^2 = -c^2-ac. Левая часть по условию >0, значит и правая тоже. Запишем -c^2-ac >0 При положительных а и с имеем положительные c^2 >0 и ac>0. Приплюсуем их и слева и справа к обеим частям неравенства. -c^2-ac + c^2 +ac > c^2+ас. Получим 0> c^2+ас, что неверно. Значит исходное b>a неверно. Поскольку а не равно b (иначе разность квадратов нулевая) , остаётся что верно только a>b.
Другой Дано a>0, b>0, a^2-b^2>0. Пусть a^2-b^2 = N >0 Тогда легко вычислить с=N/(2a+2b), причем ясно, что c>0, так как все числа положительны. Запишем тогда N=c(2a+2b) и тогда a^2-b^2 = c(2a+2b) > 0 a^2 - 2ac =b^2 +2bc Дополним левую часть до квадрата. a^2 - 2ac +с^2 =b^2 +2bc +c^2 (a-c)^2=(b+c)^2 Следовательно (a-c)=(b+c) a-b = 2c >0 a-b >0 или a>b, что и тр. док-ть.
1. Решим первое неравенство этой системы:
ответ: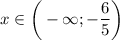
2. Дробь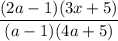 существует, если
существует, если
Перед тем как выражать , нужно рассмотреть случаи, когда дробь
, нужно рассмотреть случаи, когда дробь 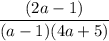 положительная, а когда отрицательная:
положительная, а когда отрицательная:
Если такая дробь положительная, то при нахождении переменнойРешим неравенство методом интервалов.
а) ОДЗ: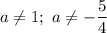
б) Нуль неравенства: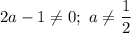
в) Решением данного неравенства будет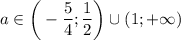 .
.
При таких значениях параметра знак неравенства меняться не будет:
знак неравенства меняться не будет:
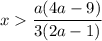
Если такая дробь отрицательная, то при нахождении переменнойРешим неравенство методом интервалов. Решением данного неравенства будет .
.
При таких значениях параметра знак неравенства изменится:
знак неравенства изменится:
ответ: если , то
, то 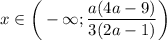 ; если
; если 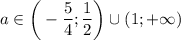 , то
, то 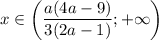 ; если
; если 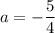 и
и 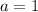 , то неравенство не имеет решений.
, то неравенство не имеет решений.
3. Данная система неравенств решается в зависимости от значений параметра , поэтому:
, поэтому:
1) Рассмотрим случай, когда решение неравенств пересекается:
Если2) Рассмотрим случай, когда решение неравенств не пересекается (когда система не имеет решений):
Оставшийся промежуток является решением этого варианта:ответ: если , то
, то 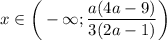 ; если
; если 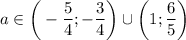 , то
, то 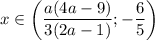 ; если
; если ![a \in \bigg[-\dfrac{3}{4}; \dfrac{1}{2} \bigg]\cup \bigg[\dfrac{6}{5}; + \infty \bigg) \cup \begin{Bmatrix} -\dfrac{5}{4}; 1 \end{Bmatrix}](/tpl/images/0595/8885/89750.png) , то система не имеет решений.
, то система не имеет решений.