Я не уверен, что правильно понял условие, но решу, так как понял:
1/3 (ква) * 0,5 (куб)
= Поскольку 2/9 это 1/3, то снизу и сверху сокращается и получается 0,5
2/9 (ква)
(куб) = 0,125
-1/2 (куб) * 2/3 (ква) - 1/8 * 4/9 - 1/18 49
= = = ___ = 2, 13/18
-1/7 (ква) -1/49 -1/49 18
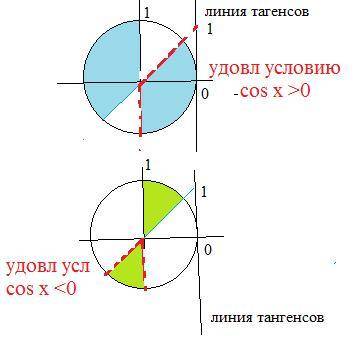
Eсли cosx > 0, т. е х в 1 и 4 четверти, делим на cosx
tgx < 1⇒ -(π/2)+πk < x < (π/4)+πk, k∈Z
Неравенству удовлетворяют корни, для которых соsx>0
Получаем
-(π/2)+2·πk < x < (π/4)+2·πk, k∈Z
Eсли cosx < 0, т. е х в 2 и 3 четверти, делим на cosx
tgx > 1⇒ (π/4)+πn < x < (π/2)+πn, n∈Z
Неравенству удовлетворяю корни, для которых соsx>0
Получаем
(3π/4)+2·πn < x < (π/2)+2·πn, n∈Z
О т в е т. Объединение ответов:
((π/2)+2·πk ; (π/4)+2·πk) U (3π/4)+2·πn ; (π/2)+2·πn), k, n∈Z
Объяснение:
M - мода вибірки, m - медіана, S - середнє значення вибірки.
M = {6, 14} , бо значення 6 і 14 трапляються найчастіше
m = 11, бо воно ділить вибірку навпіл
S = (6*2+8+10+11+13+14*2+15+23)/ 10 = 120 / 10 = 12