Сначала всё обозначим:
ширина бассейна по условию х;
длина бассейна х+6;
ширина прямоугольника,в котором находится бассейн, х + 1 (добавилось по 0,5 м с каждой стороны за счёт дорожки);
длина этого же прямоугольника х + 7 (также добавилось по 0,5 м с двух сторон за счёт дорожки).
Дальше из площади большого прямоугольника вычитаем площадь малого(бассейн) и получаем разницу 15 кв.метров - площадь всей дорожки по условию:
(x+7) *(x+1) - (x+6) * x = 15
x^2 + x + 7x - x^2 - 6x = 15 2x=8 x=4(ширина бас.); 4+6=10 (длина бас.).
ответ: 21 см
Объяснение:
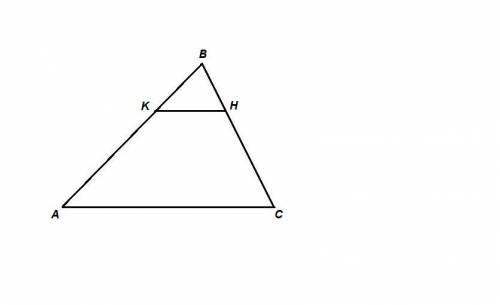
Дано: ΔАВС, КН║АС, Sakh : Sakhc = 1 : 8
Pakh = 7 см
Найти: Pabc.
Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Sakh : Sakhc = 1 : 8, значит площадь треугольника АВС составляет 9 частей, тогда
Sakh : Sabc = 1 : 9 = k²
k = 1/3
Отношение периметром подобных треугольников равно коэффициенту подобия:
Pakh : Pabc = 1 : 3
Pabc = Pakh · 3 = 7 · 3 = 21 см
S6 = 5460
Объяснение:
135=b1*q²
195= b1(q³-1)/(q-1)
b1= 135/q²
195= 135(q³-1)/q²(q-1)
13/9= (q²+q+1)/q²
9q²+9q+9=13q²
4q²-9q-9=0
D= 81+144= 225
q1= (9+15)/8= 3
q2= (9-15)/8= -0,75 - в этом случае прогрессия убывающая
q1=3, b1= 15
S6= 15*(729-1)/(3-1)= 5460