Объяснение: ЗАДАНИЕ 9 и рисунок к задаче 10 внизу на фото
ЗАДАНИЕ 10
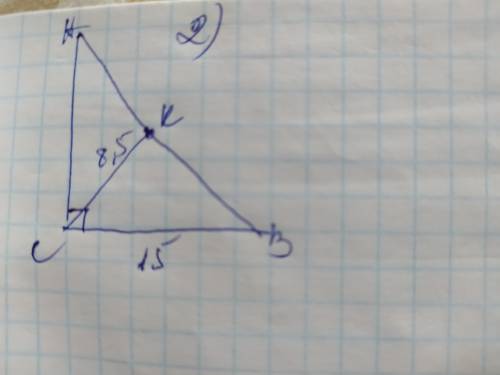
Обозначим вершины треугольника А В С с прямым углом С, катетами АС и ВС и гипотенузой АВ и медианой СК. Если медиана проведена к гипотенузе, то она проведена из прямого угла, а медиана проведённая из вершины прямого угла равна половине гипотенузы, поэтому гипотенуза АВ будет в 2 раза больше медианы: АВ=СК×2=8,5×2=17см
Пусть катет 15см будет катет ВС тогда катет АС найдём по теореме Пифагора:
АС²=АВ²-ВС²=17²-15²=289-225=64;
АС=√64=8см
Площадь треугольника найдём по формуле: S=½×AC×BC=½×15×8=60см²
ОТВЕТ: S=60см²
ЗАДАНИЕ 11
√(49-14а+а²)=√((7-а)²)=7-а
ОТВЕТ: 7-а
ЗАДАНИЕ 12
Если а=5, то: 7-а=7-5=2
ОТВЕТ: 2

очевидно что ни один из х1, х2, х3, х4 не может быть 0, (остальные тогда должны равняться 2, и 0+2*2*2=2 неверное, противоречие)
домножая первое на х1, второе на х2, третье на х3, четвертое на х4, получим
вычитая (и используя разность квадратов) получим
откуда
или
аналогично получаем другие соотношения таких же двух возможных типов соотношений между корнями
итого в общем надо рассмотреть следующие возможные комбинации (остальные дадут повтор в силу симметрии записи уравнений по переменным),
+
первое исходное уравнение
можем убедиться что (1,1,1,1) - единственное решение