(???) за 60 мин
Объяснение:
1) 1/55 кувшина за 1 мин выпивают Двалин и Бомбур
2) 1/110 кувшина за 1 мин выпивают Бомбур и Глоин
3) 1/165 кувшина за 1 мин выпивают Глоин и Двалин
4) 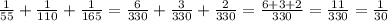
- удвоенное кол-во кувшина за 1 мин выпивают Двалин и Бомбур и Глоин
5) 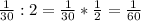
- кол-во кувшина за 1 мин выпивают Двалин и Бомбур и Глоин
6) 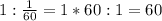
- за столько минут выпьют этот кувшин трое гномов
----------------------
ПЛОХАЯ ЗАДАЧА с кривыми данными - получается Двалин и Бомбур выпьют кувшин быстрее чем они выпьют кувшин втроем
---------------------------
=>Двалин и Бомбур выпивают 6 кувшинов компота за 330 мин, Бомбур и Глоин выпивают 3 кувшина за 330 мин, Глоин и Двалин — 2 кувшина за 330 мин.
=> 6>2+3 (если не брать в учет Глоина, для оценки)

ПРАВИЛЬНО 100%
Объяснение:1)У квадратного уравнения есть три коэффициента:
a = 1.
b = -37.
c = -27.
D = b^2 - 4ac = -37^2 - 4 * 1 * -27 = D > 0, значит у уравнения два вещественных корня (^(1/2) - это знак корня): x = (-b ± D^(1/2))/(2a).
D^(1/2) = 38,4318.
x1 = (37 + 38,4318) / (2 * 1) = 37,7159.
x2 = (37 - 38,4318 ) / (2 * 1) = -0,715879.
ответ: 37,7159, -0,715879.
2)У квадратного уравнения есть три коэффициента:
a = 1.
b = -2.
c = -9.
D = b^2 - 4ac = -2^2 - 4 * 1 * -9 = D > 0, значит у уравнения два вещественных корня (^(1/2) - это знак корня): x = (-b ± D^(1/2))/(2a).
D^(1/2) = 6,32456.
x1 = (2 + 6,32456) / (2 * 1) = 4,16228.
x2 = (2 - 6,32456 ) / (2 * 1) = -2,16228.
ответ: 4,16228, -2,16228.
3)У квадратного уравнения есть три коэффициента:
a = 2.
b = 7.
c = 6.
D = b^2 - 4ac = 7^2 - 4 * 2 * 6 = D > 0, значит у уравнения два вещественных корня (^(1/2) - это знак корня): x = (-b ± D^(1/2))/(2a).
D^(1/2) = 1.
x1 = (-7 + 1) / (2 * 2) = -1,5.
x2 = (-7 - 1 ) / (2 * 2) = -2.
ответ: -1,5, -2.
4)У квадратного уравнения есть три коэффициента:
a = 3.
b = -4.
c = -4.
D = b^2 - 4ac = -4^2 - 4 * 3 * -4 = D > 0, значит у уравнения два вещественных корня (^(1/2) - это знак корня): x = (-b ± D^(1/2))/(2a).
D^(1/2) = 8.
x1 = (4 + 8) / (2 * 3) = 2.
x2 = (4 - 8 ) / (2 * 3) = -0,666667.
ответ: 2, -0,666667.
I ВАРИАНТ II ВАРИАНТ 1. Для каких чисел определен арксинус? 1. Для каких чисел определен арккосинус? 3 ⎛ 1⎞ 2. Найти а) arcsin(−1) + arcsin ; 2. Найти а) arcsin 0 − arcsin⎜ − ⎟ ; 2 ⎝ 2⎠ ⎛ 3⎞ 3 б) arccos(−1) + arctg 3 . б) arccos⎜ − ⎟ + arcsin . ⎝ 2 ⎠ 2 3.Расположите в порядке возрастания π π arcsin (-0,5), arcsin (-0,7), arcsin . аrcсos 0,9, arcсos (-0,6), arсcos . 8 5 4.Постройте график функции (схематически) y = ⎮arcsin x⎮ y =⎮arctg x⎮
1. Д (у): ≤ 1 или х2 ≥ 1, т.е. ⎢ x2 ⎣ x ≥ 1. ⎡ π⎤ 1 2. Е (у): ⎢0; ⎥ , т.к. 2 > 0 . ⎣ 2⎦ x 3. Функция четная, т.к. у (-х) = у (х). 4. Точки пересечения: с Оу (х = 0) график не может пересекаться, т.к. функция определена толь- 1 ко при ⎮х⎮ ≥ 1; с Ох (у = 0) график пересекается в (-1; 0) и (1; 0), т.к. 2 = 1 лишь при х = ±1. x 5. В силу четности достаточно ее исследовать для х ≥ 1. 1 1 Если х = 1, то у(1) = arccos 1 = 0. Если х → + ∞, то 2 → 0 ( 2 > 0). x x 1 π 1 π Значит, arccos 2 → , причем arccos 2 < . Наименьшее у = 0 при х = ± 1, наибольшего x 2 x 2 нет. 1 6. Функция в области определения неотрицательна, т.е. arccos 2 ≥ 0. x ⎛ π⎞ ⎛ π⎞ 7. Дополнительные точки ⎜ 4 2 ≈ 1,19; ⎟ ; ⎜ 2 ≈ 1,41; ⎟. ⎝ 4⎠ ⎝ 3⎠ <Рисунок 9> В домашнее задание можно включить следующие упражнения: построить графики функ- ⎛ 1⎞ ций: y = arccos ⎜ ⎟ , y = 2 arcctg x, y = arccos ⎮x⎮. ⎝ x⎠