Объяснение:а) 2³ˣ⁺⁶ ≤ (1/4)ˣ⁻¹ , 2³ˣ⁺⁶ ≤ (2⁻²)ˣ⁻¹. 2³ˣ⁺⁶ ≤ 2²⁻²ˣ, основание показательной функции 2>1, значит функция у= 2ˣ -возрастающая, поэтому 3х+6≤2-2х ⇒ 5х≤-4 ⇒ х≤-4/5 ⇒ х≤ -0,8
б) (7/12)⁻²ˣ⁺³>(12/7)³⁺²ˣ ⇔ (12/7)²ˣ⁻³ >(12/7)³⁺²ˣ, основание показательной функции 12/7>1, значит функция у= (12/7)ˣ -возрастающая, поэтому 2х-3>3+2x 0x>6 нет реш, х=∅
в) 25⁻ˣ⁺³ ≥ (1/5)³ˣ⁻¹ ⇔(5²)⁻ˣ⁺³ ≥ (5⁻¹)³ˣ⁻¹ , 5⁻²ˣ⁺⁶ ≥ 5 ¹⁻³ˣ, основание показательной функции 5>1, значит функция у= 5ˣ -возрастающая, поэтому -2х+6≥1-3х ⇒ х≥-5, т.е. х∈[-5;+∞)
г)(5/3)²ˣ⁻⁸<(9/25)⁻ˣ⁺³ , (5/3)²ˣ⁻⁸< ((5/3)⁻²)⁻ˣ⁺³ (5/3)²ˣ⁻⁸< (5/3)²ˣ⁻⁶
основание (5/3)>1 , значит 2х-8<2x-6⇒ 0x<2? что невозможно,значит нет реш , х=∅
Объяснение:
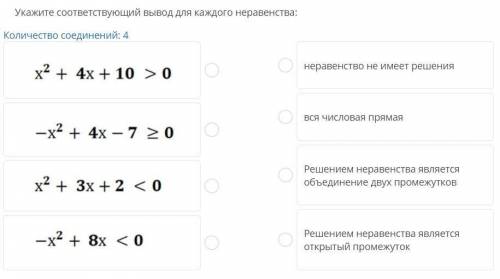
1) x² + 4x+ 10 > 0
x² + 4x+4-4+ 10 > 0
(x+2)²+6> 0- вся числовая прямая
x² + 4x+ 10 > 0 - вся числовая прямая
2) -x² + 4x - 7 > 0⇔x²-4x+7<0⇔(x²-4x+4-4+7<0⇔(x-2)²+3<0
Так (x-2)²+3>0 при ∀х, то
-x² + 4x - 7 > 0 - неравенство не имеет решения
3) x² + 3x + 2 < 0 x²+2·х·1,5+2,25- 2,25+2<0⇔(x+1,5)²-0,25<0⇔(x+1,5)²-0,5²<0⇔(x+1)(x+2)<0 ⇒x∈(-2;-1)
x² + 3x + 2 < 0 - Решением неравенства является
открытый промежуток
4) -x² + 8x < 0⇔x²-8x>0⇔x(x-8)>0
решением является: х∈(-∞;0)∪(8;+∞)
-x² + 8x < 0 - Решением неравенства является
объединение двух промежутков