Объясните, почему не существует ни одного числа b такого, что b в квадрате + 1 = 0 объясните, почему не существует ни одного числа b такого, что b в квадрате = 2а - 2 - а в квадрате найдите все значения а, при которых верно равенство а в квадрате = 0 при каком значении а существует только одно такое значение b, что а в квадрате = b в квадрате докажите, использую определения квадратного корня, что а) корень 9 = 3 б) корень 324 не равен -18 имеет ли смысл выражение? квадрат -1 при каких значениях а имеет смысл выражения? а) корень а укажите все значения переменных, при которых определено выражение: а) корень а * b б) корень х в квадрате (y-2)в квадрате
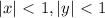
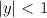 возвести в квадрат, получив,
возвести в квадрат, получив, 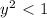 , что и требовалось проверить.
, что и требовалось проверить.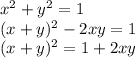
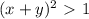
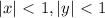 , следует, что 0 <x < 1, 0 < y < 1
, следует, что 0 <x < 1, 0 < y < 1
на третий вопрос 0 в квадрате равно ноль
4. при а равном b.