xyz=1 1/zy=x ; 1/z=xy
1/(1+y+yz)= 1/(xyz +y+yz) = 1/y*(1+z+xz) = 1/y*(xyz+z+zx)=1/zy*(1+x+xy)= x/(1+x+xy)
Аналогично: 1/(1+z+zx)= 1/(xyz+z+zx)=1/z*(1+x+xy) = xy/(1+x+xy)
Cкладываем:
1/(1+x+xy)+1/(1+y+yz)+1/(1+z+zx)= 1/(1+x+xy) +x/(1+x+xy) +xy/(1+x+xy)=
(1+x+xy)/(1+x+xy)=1
ЧТД
29641358 Не находя корней x₁ , x₂ уравнения 9x² - 24x - 20 = 0, составить уравнение четвертой степени, которое имело бы корни: x₁ , x₂, 1/x₁, 1/x₂ .
Квадратные уравнения ax² +bx + c = 0 и cx² +bx + a =0 имеют обратные корни , следовательно уравнение (9x² - 24x - 20)*( - 20x ²-24x +9) = 0 → искомое уравнение * * * можно открыть скобки * * *
D₁ = 12² - 9*(-20) =324 =18² ; * * * D₁ ' = 12² - (-20)*9 =18² =D₁ * * *
* * * x₁ =(12 -18) /9 = -2/3 , x₂=(12+18) /9 = 10/3 * * *
* * * x₃ = (12+18) /(-20) = - 3/2 = 1/x₁ ; x₄= (12- 18) /(-20) = 3/10 = 1 / x₂ * * *
От второй строки отнимем первую строку и от третьей строки отнимем первую строку. Получим
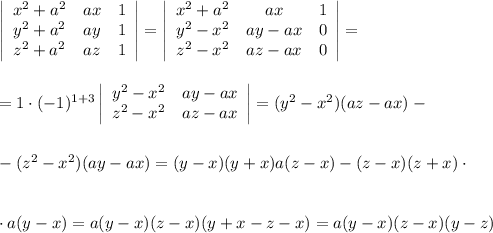
Во втором примере от четвертой строки отнимем первую строку и от второй строки отнимем третью строку и от третьей строки отнимем четвертую строку.
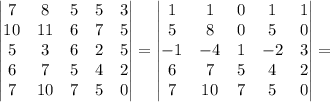
Далее сложим четвертую строку и третью строку,умноженную на (-5) и сложим пятую строку и третью строку, умноженную на (-7), получим
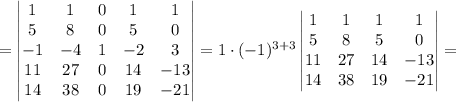
Сложим первую строку, умноженную на (-5) со второй, первую строку, умноженную на (-11) с третьей строкой и первую строку умноженную на (-14) с четвертой строкой.
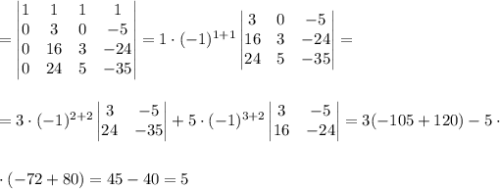
Пошаговое объяснение дано в приложении