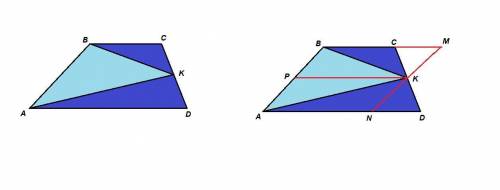
Проведем КР - среднюю линию трапеции.
Проведем MN ║ АВ через точку К. Получим параллелограмм АВMN (противоположные стороны параллельны).
CK = KD по условию,
∠КСМ = ∠KDN как накрест лежащие при ВС║AD и секущей CD,
углы при вершине К равны как вертикальные, значит
ΔСМК = ΔDNK по стороне и двум прилежащим к ней углам, значит
площадь трапеции ABCD равна площади параллелограмма ABMN.
Диагональ делит параллелограмм на два равных треугольника:
Площадь ΔКВР равна половине площади параллелограмма РВМК (верхнего),
площадь ΔКАР равна половине площади параллелограмма АРКN (нижнего), значит
площадь ΔКАВ составляет половину площади всего параллелограмма ABMN, а значит и половину площади трапеции, т.е.
Skab = Sbck + Sadk.
24 см.
Объяснение:
Пусть один катет прямоугольного треугольника будет а см , а другой bсм.
Тогда площадь равна 0,5*а* b, а квадрат гипотенузы найдем по теореме Пифагора а² + b² . Так как по условию площадь равна 24 см², а гипотенуза равна 10 см , то составляем систему уравнений:
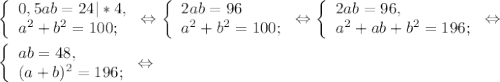

Так как a и b катеты прямоугольного треугольника , а значит положительные числа .Тогда их сумма не может быть отрицательным числом. Поэтому вторая система не подходит по смыслу задачи.
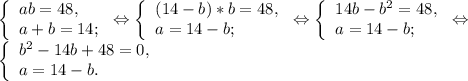
Решим квадратное уравнение:
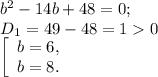
Если b=6, то а=8
Если b=8, то а=6
Значит катеты прямоугольного треугольника 6 см и 8 см. Тогда периметр ( сумма длин всех сторон треугольника)
P= 6+8+10 = 24 (см)
ответ: 43, см фото.
Объяснение: