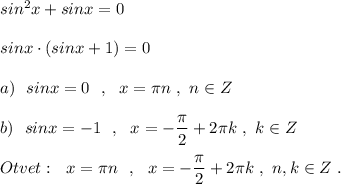
Радиус проведённый в точку касания перпендикулярен касательной.
В четырёхугольнике сумма углов равна 360°.
В четырёхугольнике EOFC:
∠ECF = 360°-∠EOF-∠CEO-∠CFO = 360°-102°-90°-90° = 78°.
В треугольнике сумма углов равна 180°.
В ΔABC:
∠BAC = 180°-∠ABC-∠BCA = 180°-90°-78° = 12°
В четырёхугольнике BEOD:
∠EOD = 360°-∠ODB-∠DBE-∠BEO = 360°-90°-90°-90° = 90°
В четырёхугольнике DOFA:
∠DOF = 360°-∠OFA-∠FAD-∠ADO = 360°-90°-12°-90° = 168°
ответ: ∠A=12°, ∠C=78°, ∠EOD=90° и ∠FOD=168°.
Объяснение:
Не знаю, может и не правильно.
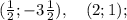
Объяснение:
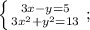
Выражаем из верхнего уравнения переменную "у":
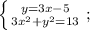
Подставляем полученное выражение в нижнее уравнение вместо "у":
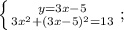
Раскрываем квадрат разности двух выражений, пользуясь следующей формулой:
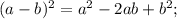
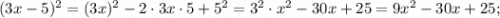
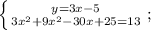
Приведём подобные слагаемые. Для этого вынесем общий множитель за скобки:
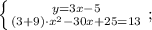
Выполним сложение в скобке и перенесём слагаемое 13 со знаком минус в левую часть уравнения:
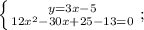
Выполним вычитание:

Разделив все части нижнего уравнения на 6, получим:

Теперь разделим все части нижнего уравнения на 2 для того, чтобы получить приведённое квадратное уравнение:
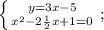
Решаем нижнее уравнение по теореме Виета. Согласно ей, сумма корней приведённого квадратного уравнения равна коэффициенту при "х", взятому с противоположным знаком, а их произведение — свободному члену:
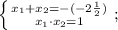
Минус перед скобкой и минус после скобки дают плюс:
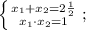
Корнями этой системы являются числа 1/2 и 2.
Мы нашли два значения переменной "х". Теперь подставим каждое из них в верхнее уравнение:
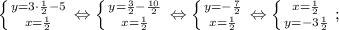
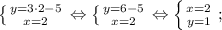
Мы получили две пары корней:
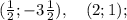
Они являются решениями системы.