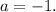Известно, что площадь прямоугольника равна произведению ширины на длину. Пусть: длина прямоугольника - x ширина прямоугольника - y Тогда плошадь прямоугольника равна x*y Получим систему уравнений:
1) x = 2+y 2) x*y - (x+2)*(y-4) = 40
В первом уравнении, длина больше ширины на 2 см. Во втором уравнении, разность площадей равна 40. Раскроем скобки во втором уравнении и приведём подобные члены: x*y - (x*y - 4x + 2y - 8) = 40 x*y - x*y + 4x - 2y + 8 = 40 4x - 2y = 40-8 4x - 2y = 32 (разделим на 2, получим далее) 2x - y = 16
Теперь решим эту систему уравнений:
x = 2+y 2x - y = 16
Подставим x = 2+y во второе уравнение: 2*(2+y) - y = 16 2y + 4 - y = 16 y = 12 (см) - ширина. x = y+2 = 14 (см) - длина.
Известно, что площадь прямоугольника равна произведению ширины на длину. Пусть: длина прямоугольника - x ширина прямоугольника - y Тогда плошадь прямоугольника равна x*y Получим систему уравнений:
1) x = 2+y 2) x*y - (x+2)*(y-4) = 40
В первом уравнении, длина больше ширины на 2 см. Во втором уравнении, разность площадей равна 40. Раскроем скобки во втором уравнении и приведём подобные члены: x*y - (x*y - 4x + 2y - 8) = 40 x*y - x*y + 4x - 2y + 8 = 40 4x - 2y = 40-8 4x - 2y = 32 (разделим на 2, получим далее) 2x - y = 16
Теперь решим эту систему уравнений:
x = 2+y 2x - y = 16
Подставим x = 2+y во второе уравнение: 2*(2+y) - y = 16 2y + 4 - y = 16 y = 12 (см) - ширина. x = y+2 = 14 (см) - длина.
Задача. При каких значениях параметра система
система
имеет бесконечное множество решений?
Решение. Система линейных уравнений, которая имеет вид
допускает три варианта решений:
1. Имеет одно решение:
2. Не имеет решений:
3. Имеет бесконечное количество решений:
Таким образом, заданная система линейных уравнений будет иметь бесконечное количество решений, если:
Следовательно, нужно рассмотреть три пары уравнений, из которых нужно выбрать корень (корни), который встречается у всех трех уравнений:
Значит, при все три выражения равны друг другу, откуда делаем вывод, что данная система будет иметь бесконечное количество решений.
все три выражения равны друг другу, откуда делаем вывод, что данная система будет иметь бесконечное количество решений.
ответ: