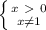
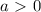 .
.![\sqrt[10]{ a^{8} x^{0,25} - x^{0,25} x^{ log_{x} a^{x} } - a^{8 + 0,25} + a^{x} a^{0,25} } = \\ \sqrt[10]{ a^{8} x^{0,25} - x^{0.25} a^{x} - a^{8} a^{0,25} + a^{x} a^{0,25} } = \\ \sqrt[10]{(a^{8} x^{0,25} - x^{0.25} a^{x}) - (a^{8} a^{0,25} - a^{x} a^{0,25})} = \\ \sqrt[10]{ x^{0,25} (a^{8} - a^{x}) - a^{0,25}(a^{8} - a^{x})} = \\ \sqrt[10]{( a^{8} - a^{x} )( \sqrt[4]{x} - \sqrt[4]{a}) }](/tpl/images/0776/0632/5ac76.png)
![( a^{8} - a^{x} )( \sqrt[4]{x} - \sqrt[4]{a} ) \geq 0](/tpl/images/0776/0632/80786.png)
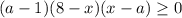
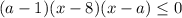
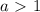 . Тогда
. Тогда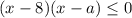
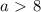
![[8,a]](/tpl/images/0776/0632/1c0af.png)
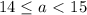 . Правый конец не включаем, поскольку при a = 15 в области определения будет лежать и восьмая целая точка.
. Правый конец не включаем, поскольку при a = 15 в области определения будет лежать и восьмая целая точка.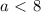 , а с учётом рассматриваемых а,
, а с учётом рассматриваемых а, 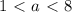 . Тогда точка x = 8 лежит правее точки x = a и решение неравенства будет иметь вид:
. Тогда точка x = 8 лежит правее точки x = a и решение неравенства будет иметь вид: ![[a, 8]](/tpl/images/0776/0632/8e143.png) .
. 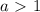 , то
, то 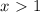 заведомо. Оба ограничения здесь выполняются, а потому указанный отрезок и есть область определения нашей функции.
заведомо. Оба ограничения здесь выполняются, а потому указанный отрезок и есть область определения нашей функции. ![(1,2]](/tpl/images/0776/0632/7dff9.png) . Правый конец обязан входить, а вот левый обязан не входить, поскольку иначе на отрезке будет 8 целых точек. Поскольку все эти значения больше 1, то эти интервалы пойдут в ответ.
. Правый конец обязан входить, а вот левый обязан не входить, поскольку иначе на отрезке будет 8 целых точек. Поскольку все эти значения больше 1, то эти интервалы пойдут в ответ.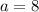 . Тогда получаем неравенство
. Тогда получаем неравенство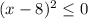 , которое, очевидно, выполняется лишь в одной точке(x = 8). Значит, a = 8 условию задачи не удовлетворяет.
, которое, очевидно, выполняется лишь в одной точке(x = 8). Значит, a = 8 условию задачи не удовлетворяет.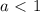 . Тогда
. Тогда 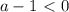 и неравенство преобразуется так:
и неравенство преобразуется так: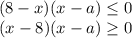
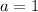 . Тогда a - 1 = 0 и неравенство имеет вид
. Тогда a - 1 = 0 и неравенство имеет вид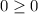
 ∈
∈![(1,2]](/tpl/images/0776/0632/7dff9.png) ∪
∪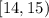
Основание логарифма больше 0 и не равно 1.
А подлогарифмическое выражение должно быть больше 0.
Разберемся с последним неравенством.
Это неравенство легко решить методом интервалов.
Найдем нули функции:
Отсюда вытекают 3 случая.
(рассматривать случай при а от 0 до 1 нет смысла, так как область определения в это случае будет в границах от 0 до 1, и 4 целых чисел тут не наберется)
Первый случай:
В этом случае при любых значениях а в рассматриваемом промежутке не будет 4 целых чисел в области определения.
Второй случай:
При а = 5 вовсе не будет никакой области определения, так как
Третий случай:
В этом случае можно выделить те значения а при которых область определения функции будет содержать ровно 4 целых числа.
ответ: