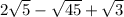Надо помнить, что логарифм отрицательного числа и нуля не существует. Поэтому, чтобы найти область определения, надо решить неравенство:
x^2 - 2x больше нуля.
Корни квадратичной функции 0 и 2. На числовой прямой ставим эти числа. Вся числовая прямая разбилась на интервалы:
(- бесконечность ; 0]; [0; 2]; [ 2 ; + бесконечность)
Надо определить знак нашей квадратичной функции на кадом интервале. Знаки будут такие: +; -; +
ответ: х∈( - бесконечность; 0)∨(2; плюс бесконечность)
Объяснение:
В решении.
Объяснение:
2) Пусть аn есть арифметическая прогрессия. Если а1=-10 и а3=-4, с характеристического свойства найдите а2. Определите значение девятого члена прогрессии.
а) а₁ = -10;
а₃ = -4;
а₂ = ?
а₂ = (а₁ + а₃)/2
а₂ = (-10 - 4)/2
а₂ = -14/2
а₂ = -7;
б) a₉ = ?
an = a₁ + d(n - 1);
а₉ = а₁ + d(n - 1);
Найти d:
d = a₂ - a₁;
d = -7 - (-10)
d = -7 + 10
d = 3;
а₉ = а₁ + d(n - 1);
а₉ = (-10) + 3(9 - 1)
а₉ = (-10) + 24
а₉ = 14.
3) в арифметической прогрессии (аn) известно, что d=2,a1=5. Найти s13.
а₁ = 5;
d = 2;
S₁₃ = ?
Формула:
Sn = ((2a₁ + d(n - 1))/2 * n
S₁₃ = (2 * 5 + 2 * 12)/2 * 13
S₁₃ = (10 + 24)/2 * 13
S₁₃ = 17 * 13
S₁₃ = 221.
Упростите выражение
Решение и ответ: