ответ:Алгебра - раздел, который изучает операции над элементами множеств, обобщает эти операции. Геометрия - раздел, который изучает пространственные структуры, их отношения, и обобщает их. В алгебре обязательно знать математические законы и максимально внимательно производить все вычисления.
Также в геометрии приращении задач надо использовать теоремы и приводить как можно больше доказательств. В алгебре, в большинстве встречаются примеры уравнения и функции, в ней нужно перемножать большое количество цифр, преобразовывать функции. В геометрии нужно находить величину и площади объектов, доказывать и обосновывать что за фигура перед тобой, находить длину отрезков без линеек. Вывод: геометрия изучает фигуры и задачи, а алгебра примеры и уравнения.
a ∈ ∅
Объяснение:
Графиком трехчлена в левой части является парабола. В таком случае, условие "меньше 0" означает, что график лежит целиком под осью абсцисс, а ветви параболы направлены вниз ( a<0 ).
Если график лежит целиком под осью абсцисс, то нет пересечения графика с осью x, что равносильно отсутствию действительных корней квадратного трехчлена (дискриминант меньше 0).
Т.к. ветви параболы направлены вниз, то параметр a можно представить в виде:
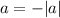
Тогда дискриминант равен:
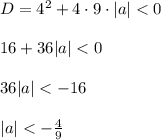
Получили противоречие (модуль не может быть отрицательным).
Значит не существует такого параметра a, при котором неравенство будет верно при любых значениях x
Жылы математика, бір теорема болды есеп болып табылады дәлелдеді , басқа да теоремалар және жалпы қабылданған есептілігі: бұрын белгiленген есептілігі негізінде аксиомалары[ дереккөзі анықталмаған 295 күн ] . Басқаша айтқанда, теорема - бұл математикалық тұжырым, оның ақиқаттығы дәлелдеу арқылы анықталады [2] . Теорема - аксиомалардың логикалық нәтижесі . Математикалық теореманың дәлелі - бұл формальды жүйенің ережелеріне сәйкес келтірілген теореманың тұжырымының логикалық аргументі . Теореманың дәлелденуі көбінесе теорема тұжырымының ақиқаттығын дәлелдеу ретінде түсіндіріледі. Дәлелденетін теоремаларға қойылатын талапты ескере отырып, теорема ұғымы тәжірибелік сипаттағы ғылыми заң тұжырымдамасынан айырмашылығы түбегейлі дедуктивті болып табылады [3] .
Алгебра - это раздел, который изучает операции над элементами множеств, обобщает эти операции. Геометрия - это раздел, который изучает пространственные структуры, их отношения, и обобщает их. В алгебре обязательно знать математические законы и максимально внимательно производить все вычисления.