Найдем вероятность того, что у определенного работника взятая деталь стандартная (как отношение соответствующего числа стандартных деталей к общему числу деталей):
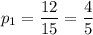
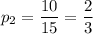
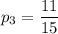
Поскольку события выбора по одной детали у каждого из работников независимы, то вероятность выбора у всех рабочих стандартных деталей определяется произведением вероятностей:
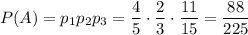
Найдем вероятности выбора нестандартных деталей у каждого работника:
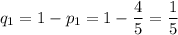
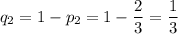
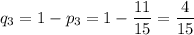
Одна стандартная деталь может быть выбрана только у первого работника, только у второго или только у третьего. Вероятность каждого из событий находится как произведение одной вероятности выбора стандартной детали на две другие вероятности выбора нестандартных деталей. Поскольку такие события несовместны, то полученные вероятности необходимо сложить.
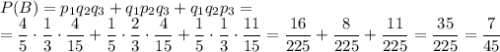
ответ: А) 88/225; Б) 7/45
б) (x + 7)2 — 10x = x2 + 14x + 49 — 10x = x2 + 4x + 49;
в) 9x2 — (с + 3x)(с — 3x) = 9x2 — с2 + 9x2 = 18x2 — с2;
г) 5b2 — (а — 2b)2 = 5b2 — а2 + 4аb — 4b2 = b2 + 4аb — а2;
2. а) (а — с) (а + с) — (а — 2с)2 = а2 — с2 — а2 + 4ас — 4с2 = 4ас — 5с2;
б) (x + 3)2 — (x —3)2 = x2 + 6x + 9 — x2 + 6x — 9 = 12x;
в) (а + 3с)2 + (b + 3с)(b — 3с) = а2 + 6ас + 9с2 + b2 — 9с2 = а2 + 6ас + b2;
г) (x — 4у)2 + (x + 4у)2 = x2 — 8xу +16у2 + x2 + 8xу + 16y2 = 2x2 + 32у2;
д) (x —3)(x+3) —(x+8)(x —8) = x2 —9—x2+64 = 55;
е) (2а + 1)(2а — 1) + (а — 7)(а + 7) = 4а2 — 1 + а2 — 49 = 5а2 - 50.