Если вписать квадрат в окуржность, то его диагональ будет диаметром этой окружности (угол опирающийся на диаметр - прямой). Таким образом длина диагонали квадрата вписанного в окружность: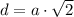 
, где a - сторона квадрата. Так как диагональ есть диаметр то она равна двум радиусам: 
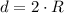. Тогда выразим длину стороны квадрата: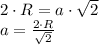 
Если вписать окружность в квадрат, то ее радиус будет равен половине стороны квадрата: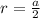 
. Подставив предыдущую формулу в данную, получим: 
.
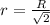Таким образом мы получили бесконечно убывающую геометрическую прогрессию радиусов окружностей. Первый элемент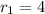 
, знаменатель прогресии 
.
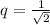Сумма всех радиусов равна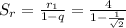 
.
Тогда сумма длин всех окружностей: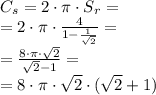 
возьмём стороны прямоугольника за х, тогда:
(3х + 5х) × 2 =40
6х+10х=40
16х=40
х=2.5
1 сторона = 2.5 × 3 = 7.5(см)
2 сторона = 2.5 × 5 = 12.5(см)