а).
Просто подставляем в уравнение, задающее функцию,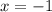 
:
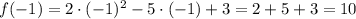
б).
Найдем те значения 
, при которых значение функции становится равным 
:
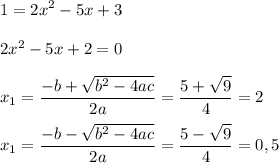
в).
Для того, чтобы определить, принадлежит ли точка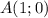 
графику, подставим в уравнение функци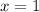и 
и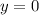 
, и посмотрим, что получится:
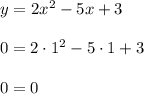
Получилось верное равенство! Значит, точка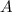 
действительно принадлежит графику рассматриваемой функции.
___________________________________________
Задание № 2.а).
Задача заключается в решении неравенства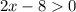 
:
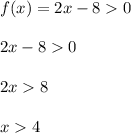
Получаем, что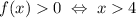 
, или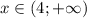 
.
б).
Ноли функции - это те значения , при которых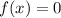 
:
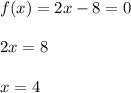
Значит, единственный ноль функции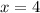 
.
___________________________________________
Задание № 3.а).
Область определения функции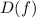 
- это те значения , при которых функция существует.
А функция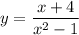 
существует только в том случае, если ее знаменатель не равен нолю:
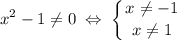
То есть, область определения данной функции - все действительные , кроме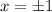 
:
Задача решена!
Функция задана формулой f(x) = 2x² - 5x + 3
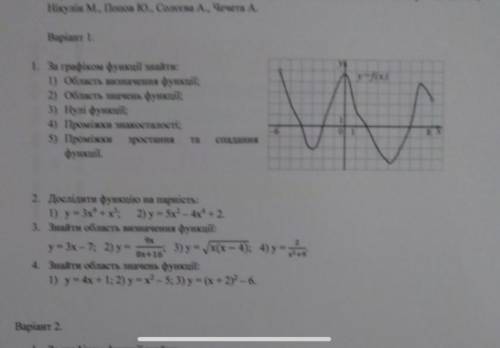
a)Найдите f(-1)
f(-1) = 2 * (-1)² - 5 * (-1) + 3 = 2 * 1 + 5 + 3 = 2 + 8 = 10
ответ: 10
б) Определите, при каких значениях X выполняется равенство f(x)=1
f(x)=1
2x² - 5x + 3 = 1
2x² - 5x + 2 = 0
D = b² - 4ac = 25 - 4 * 2 * 2 = 9
x₁ = (-b-√D)/2a = (5 - 3)/4 = 0,5
x₂ = (-b+√D)/2a = (5 + 3)/4 = 2
ответ: при x = 0,5 и x = 2.
в) Принадлежит ли графику функции точка A(1;0).
0 = 2 * 1² - 5 * 1 + 3
0 = 2 - 5 + 3
0 = 0
Значит, точка A(1;0) ∈ графику функции.
Функция задана формулой f(x) = 2x - 8
a) Определите, при каких значениях x f(x) > 0.
f(x) > 0
2x - 8 > 0
2x > 8
x > 4
При x ∈ (4; +∞) функция больше 0.
ответ: при x ∈ (4; +∞)
б) Найдите нули функции.
Нуль функции - место, где график функции пересекается с осью Ох. Приравняем к 0:
2x - 8 = 0
2x = 8
x = 4
ответ: 4
Найдите область определения функции:
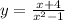
Найти область определения функции - значит найти значения, при которых функция имеет смысл.
Заметим, что если знаменатель будет равен нулю - функция бессмысленна. Тогда:
x² - 1 ≠ 0
x² ≠ 1
x ≠ ± 1
Область определения (ОДЗ): x ∈ ( - ∞; -1) ∪ (-1; 1) ∪ (1; + ∞).
1. 1)D(y)=(-6;8)
2)E(y)=[-3.4; 5)
3) нули х=-4; х=-2; х=2; х=6
4) у>о при х∈(-6;-4)∪(-2;2)∪(6;8); у<о при х∈(-4;-2)∪(2;6)
5) функция возрастает при х∈[-3; 0] и при х∈ [4;7]; убывает
при х ∈ (-6;-3]; [0;4]; [7;8]
2. 1) у=3х⁹+х³- нечетная,
т.к. х; -х∈D(у) и у(-х)=3*(-х)⁹+(-х)³=-3х⁹-х³=-(3х⁹+х³)=-у(х)
2) у=5х²-4х⁴+2- четная, т.к. х; -х∈D(у) и
у(-х)=5*(-х)²-4*(-х)⁴+2=5х²-4х⁴+2=у(х)
3. 1) х- любое действительное число.
2)х≠-2, иначе знаменатель обратится в нуль, а на нуль делить нельзя. можно и так написать х∈(-∞;-2)∪(-2;+∞)
3)х*(х-4)≥0, решим методом интервалов. х=0, х=4
___04
+ - +
х∈(-∞;0]∪[4;+∞)
4)у=2/(х²+9) знаменатель не обращается в нуль ни при каких значениях х, т.к. х²≥0, а 9- число положительное, поэтому областью определения служит любое число , т.е. х∈(-∞;+∞)