Объяснение:
1) (х²-8х-9)/(х-8)=0;
Домножим обе части уравнения на (х-8).
О.Д.З.: х-8≠0, х≠8.
х²-8х-9=0;
D₁=к²-ас;
D₁=4²+1*9=16+9=25=5²;
х₁₂=(-к±√D₁)/а;
х₁₂=(4±5)/1;
х₁=9; х₂= -1.
Если х=9, то х-8≠0.
Если х= -1, то х-8≠0.
ответ: -1; 9.
2) (х²-49)/(х+7)=0;
О.Д.З.: х+7≠0; х≠ -7.
Домножим обе части уравнения на (х+7).
х²-49=0;
(х+3)(х-3)=0,
х= -3; х=3.
Если х= -3, то х+7≠0.
Если х= 3, то х+7≠0.
ответ: -3; 3.
3) х²/(х-1)=(2х-1)/(х-1);
О.Д.З.: х-1≠0; х≠1.
Домножим обе части уравнения на (х-1).
х²=2х-1;
х²-2х+1=0;
(х-1)²=0;
х=1.
Если х= 1, то х-1=0.
ответ: нет решений.
Ремарка:
в большинстве случаев использовалась расширенная теорема Виета, которая есть не что иное как счелканье уравнений как семечек в уме. Я рекомендую вам изучить очень хорошо метод переброски, который, поверьте моему опыту, упростит вам жизнь.
Объяснение:
1)
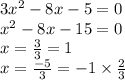
2)
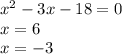
3)
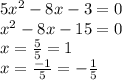
4)
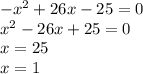
5)
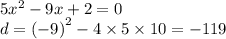
То есть уравнение корней не имеет, так как дискриминант отрицательный.
6)
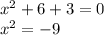
Уравнение корней не имеет, так как какое бы мы число к квадрату не поднесли, результат всегда будет положительный, а не отрицательный, как вот (-9).
7)
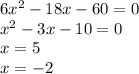
8)
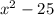
Если задача стоит разложить на множители, то имеем:
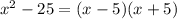
Если задача стоит найти корни уравнения, то имеем:
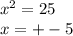
9)
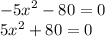
Уравнение не имеет корней, так как левая часть всегда > 0, а не равна ему. Действительно, какое бы мы число не подставили вместо x, оно всегда будет ≥ 80.
10)
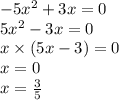
11)
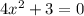
Уравнение не имеет корней, аналогичная ситуация как в уравнении 9.
12)
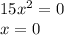
1) х(2a-5b)+y(2a-5b)=(2a-5b)*(x+y)
2) 5x(b-c)-(c-b)=5x*(b-c)-(-(b-c))=5x*(b-c)+(b-c)=(b-c)*(5x+1)
3) (x-5)(2y+4)-(x-5)(4y+1)=(x-5)*(2y+4-(4y+1))
(x-5)*(2y+4-4y-1)=(x-5)*(-2y+3)
1) y^2-5y=0=y*(y-5)=0
у=0
у-5=0;у=5
у1=0; у2=5
2) х^2+4х=0=х*(х+4)=0
х=0
х+4=0;х=-4
х1=-4; х2=0
1) 8^6+2^15=294912
294912:9=32768
2) 14^4-7^4=36015
36015:5=7203