No1 Даны числовые ряды:
1. 21, 14, 8, 14, 13, 10, 14, 8, 13, 15.
2. 10, 12, 8, 12, 14, 10, 12, 8, 12, 15
Найдите среднее арифметическое, моду, медиану и размах этих рядов.
No2
Даны два набора чисел: 3, 6, 12 и 5, 9, 9, 13. У какого набора медиана больше и на
сколько? У какого набора больше размах и на сколько?
No3
1. По данным выборки 8, 9, 10, 9, 6, 10, 6, 5, 9 определите, на сколько отличается
среднее арифметическое от медианы?
2. По данным выборки 7, 8, 9, 5, 7, 5, 9, 5, 8 определите, на сколько отличается
среднее арифметическое от медианы
No4
В ряду чисел 2, 7, 10, __, 18, 19, 27 одно число оказалось стертым. Восстановите его, зная,
что среднее арифметическое этого ряда чисел равно 14.
No5
Возвести одночлен в степень:
а) (5b6)2 в) (2у10у)3
б) (–3а5 b)3 г) (–3
4k6р3)2
No6 Записать выражение в виде одночлена стандартного вида:
а) 5 · (3mn) · (6m) в) 6 · (3kbc) · (- 5pkc)
б) 53ab2(-4)3ab г) 3ab7·4a9b2b
люди
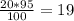(кг) - питательные вещества в изюме
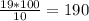(кг) - виноград
разложим по схеме горнера:
6x^3-25x^2+3x+4 нужно перебрать все числа, на которые делится число 4, это 1,-1,2,-2,4,-4
нужно подставлять их вместо х и выбрать то число, при котором выражение равно 0!
в данном случае это число 4 (k=4)
6*64-25*16+12+4=384-400+12+4=0
теперь составляем таблицу:
6 -25 3 4 (- это коэф. 6x^3-25x^2+3x+4)
k=4(x-4) 6 4*6+(-25)=-1 -1*4+3=-1 -1*4+4=0
получим:(x-4)(6x^2-1x-1)
теперь осталось разложить 6x^2-1x-1 с дискриминанта:
D=1+24=25;
x1=1+5/12=1/2; x2=1-5/12=-1/3
(x-4)(x-1/2)(x+1/3)