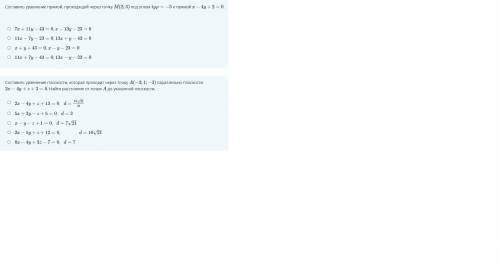
1 .Угловой коэффициент данной прямой к₁=1/4, т.к. у=х/4+1/2;
угловой коэффициент - это тангенс угла наклона прямой с положительным направлением оси абсцисс.
к₂=-3, угол пересечения прямых β связан с к₁ и к₂ уравнением
tgβ=(к₁-к₂)/(1+к₁*к₂)=(1/4-(-3)/(1+(1/4)*(-3))=(13/4)*4=13, искомая прямая имеет вид у=13х+b, найдем b, используя условие прохождения этой прямой через точку М(2;3)
3=2*13+b,⇒b=-23; или в общем виде 13х-у -23=0
ответ последний в списке ответов. 13х-у -23=0
2. нормальный вектор данной плоскости →n(2;-4;1)
т.к. плоскости - данная и искомая - параллельны, то нормальным вектором искомой плоскости тоже будет вектор →n(2;-4;1), уравнение искомой плоскости запишем в виде
2*(х-(-3))-4*(у-1) +1*(z-(-3 ))=0, или после упрощения
2х+6-4у+4+z+3=0
2х-4у+z+13=0 - первый в списке ответов.
расстояние от точки А(-1; 3; -1) до плоскости 2х-4у+z+3=0 найдем по формуле расстояния от точки А(х;у;z) до плоскости ах+bу+сz+d=0;
d = |а·Аx +b·Аy + c·Аz + d|/√(а²+b² +c²)
d=I2*(-3)-4*1+1*(-3)+3I/√(2²+(-4)²+1²)=10/√21=10√21/21
ответ
2х-4у+z+3=0
10√21/21
Объяснение:
Функция задана формулой y=-3x+1
1)значении функции если значение аргумента ровно 4 ?
2)значения аргумента , при котором значение функции равно -5
2)проходит ли график функции через точку А(-2;7)
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблица:
х -1 0 1
у 4 1 -2
а)Чтобы найти значение у, нужно известное значение х подставить в уравнение и вычислить у:
х=4
у= -3*4+1= -11 при х=4 у= -11
б)Чтобы найти значение х, нужно известное значение у подставить в уравнение и вычислить х:
у= -5
-5= -3х+1
3х=1+5
3х=6
х=2 у= -5 при х=2
в)Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение, если левая часть будет равна правой, значит, точка принадлежит графику и наоборот.
A (−2; 7)
y = −3x + 1
7= -3*(-2)+1
7=6+1
7=7, проходит.
Решение системы уравнений х=10
у=12
Объяснение:
Решить систему уравнений.Методом алгебраического сложения.
x/5-y/6=0
5x-4y=2
Нужно избавиться от дробного выражения в первом уравнении, общий знаменатель 30, надписываем над числителями дополнительные множители:
6*х-5*у=0
6х-5у=0
5х-4у=2
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, коэффициенты или при х, или при у были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают одно из уравнений, как бы подгоняют ко второму, можно умножать обе части уравнения на одно и то же число, делить.
Поэтому первое уравнение умножим на -5, а второе на 6:
-30х+25у=0
30х-24у=12
Складываем уравнения:
-30х+30х+25у-24у=12
у=12
Теперь подставляем значение у в любое из двух уравнений системы и вычисляем х:
5х-4*12=2
5х-48=2
5х=2+48
5х=50
х=10
Решение системы уравнений х=10
у=12
Объяснение:
x-4y+2=0 M(2;3) tgα=-3.
Запишем прямую х-4у+2=0 в виде уравнения у=kx+b с угловым коэффициентом k:
Значит угловой коэффициент данной прямой k=0,25.
Геометрический смысл углового коэффициента:
k=tg α, где α– угол наклона прямой у=kx+b c положительным направлением оси Ох.
При пересечении двух прямых у=k₁x+b₁ и у=k₂x+b₂: k₁=tg α₁, k₂=tg α₂,
а угол между прямыми α=α₁–α₂. ⇒
По формуле тангенса разности двух углов:
ответ: 13x-y-23=0.