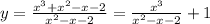
1. Область определения:
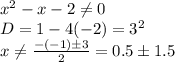
x∈(-∞;-1)∪(-1;2)∪(2;+∞)
2. Функция общего вида.
3. Найдём точки пересечения с осями:
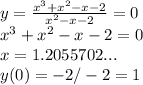
4. Исследование с первой производной:
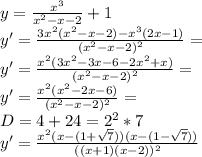
Cм. внизу.
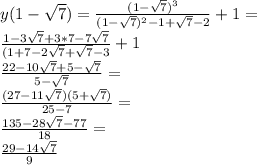
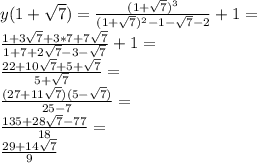
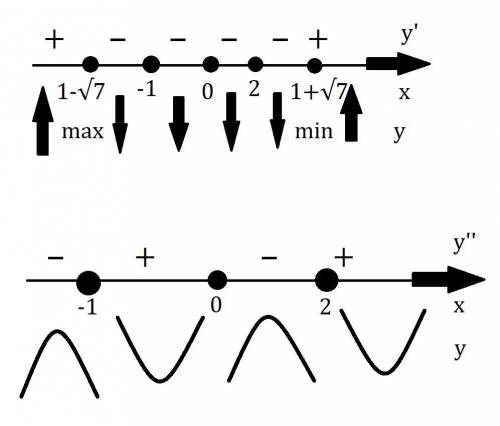
5. Исследование с второй производной:
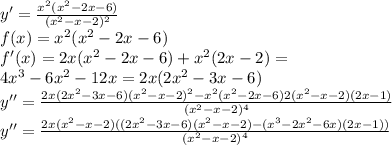
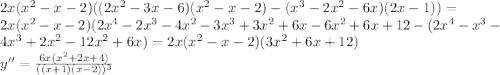
Выражение в скобках в числителе всегда положительное и не равняется нулю, см. внизу.
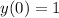
6. Уравнение асимптот:
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты: 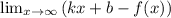
Находим коэффициент k: 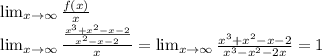
Находим коэффициент b: 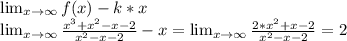
Получаем уравнение наклонной асимптоты: у=x+2
Найдем вертикальные асимптоты. Для этого определим точки разрыва: 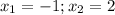
Находим переделы в точке x=-1

Это точка разрыва II рода и является вертикальной асимптотой.
Находим переделы в точке x=2

Это точка разрыва II рода и является вертикальной асимптотой.
Відповідь:D(y) = (- бесконечности; -1] объединения [5;+бесконечности)
Пояснення:
5+4x-x^2>0
x^2-4x-5<0
x=-1 x=5
Воспользовавшись методом интервалов видим, что:
х Є (- бесконечности; -1] объединения [5;+бесконечности)
Отсюда:
D(y) = (- бесконечности; -1] объединения [5;+бесконечности)