(508) Учащимися 8 классов одной из школ показаны следующие результаты в подтягивании на перекладине: 9; 5; 7; 10; 11; 10; 14; 7; 10; 11; 8; 10; 8; 9; 12; 13; 8; 11; 9; 9; 10; 6; 9; 13; 9; 17; 11; 15; 8. По этим данным составьте вариационный ряд с интервалом, равным 2, распределения учащихся по количеству подтягиваний и найдите накопленные частоты , соответствующие каждому интервалу
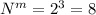
((3*(cosx-1))/(sin(π/2-x))*(((sin(π/2+x)+1)/(sin(x-3π/2))
1. (3*(cosx-1))/(sin(π/2-x))=(3*(cosx-1))/(cosx)) использовали формулу приведения, от синуса х перешли к косинусу х;
2. опять применим формулы приведения и нечетность синуса.
((sin(π/2+x)+1)/(sin(x-3π/2))=(cosx+1)/(-sin(3π/2-x)=(cosx+1)/(-(-cosx))=
((cosx+1)/(cosx))
3. Перемножим полученные выражения. здесь еще раскроем числитель по формуле разности квадратов. (а-в)(а+в)=а²-в²
(3*(cosx-1))/(cosx))*((cosx+1)/(cosx))=((3*(cosx-1))(cosx+1))/((cosx)*(cosx))
3*(cos²x-1)/cos²x=-3*sin²x/cos²x=-3tg²x; при х=π/6 получим -3tg²(π/6)=
-3*(1/√3)²=-3/3=-1;