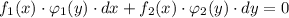
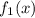 и
и 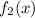 зависят только от переменной "х" , а функции
зависят только от переменной "х" , а функции 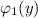 и
и 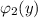 зависят только от переменной "у" . Указывается на то, что диффер. уравнение допускает обособление (разделение) переменных только тогда, когда перед дифференциалами (dx и dy) стоят функции, являющиеся произведениями двух других функций, одна из которых зависит только от "х" , а вторая зависит только от "у" .
зависят только от переменной "у" . Указывается на то, что диффер. уравнение допускает обособление (разделение) переменных только тогда, когда перед дифференциалами (dx и dy) стоят функции, являющиеся произведениями двух других функций, одна из которых зависит только от "х" , а вторая зависит только от "у" . 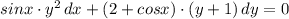 .
. 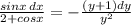 .
.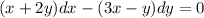 , то переменные уже нельзя разделить, так как нельзя функции, стоящие перед dx и dy,представить в виде произведения
, то переменные уже нельзя разделить, так как нельзя функции, стоящие перед dx и dy,представить в виде произведения 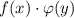 .
.
Мінімальна відстань від точки до прямої — це перпендикуляр, тому K має бути основою перпендикуляра від точки K на пряму 6x-8y-17=0.
Знайдемо кутовий коефіцієнт (далі — КК) заданої прямої:
КК перпендикулярних прямих пов'язані співвідношенням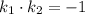 , тому КК перпендикуляра дорівнює:
, тому КК перпендикуляра дорівнює:
Рівняння прямої з КК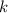 , яка проходить через точку
, яка проходить через точку 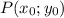 , має вигляд:
, має вигляд:
Щоб знайти координати точки K, складемо систему з рівнянь двох прямих:
Итак, координаты точки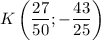 . Найдём |PK|:
. Найдём |PK|:
Відповідь: 4,1 од.