Двое рабочих, работая вместе, могут выполнить задание за 6 часов. За сколько часов может выполнить задание каждый рабочий, если один из них может это сделать на 5 часов быстрее второго?
А V t
1 раб. 1 1/х х час
2 раб. 1 1/(х+5) х+5 час
1+2 раб 1 1/6 6 час
где А- работа, V производительность труда, t- время
быстрее работает 1 раб = х час, второй на 5 час. дольше х+5
составим уравнение
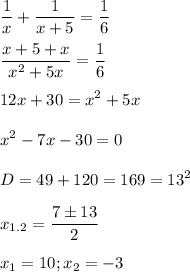
тогда работу первый раб. выполнит за 10 час
второй раб. за 15 час
(x² - 2x)² -2(x - 1)² - 1 = 0
(x² - 2x)² - 2(x² - 2x + 1) - 1 = 0
Пусть x² - 2x = t, тогда получаем
t² - 2(t + 1) - 1 = 0
t² - 2t - 3 = 0
По т. Виета:
t1 = -1
t2 = 3
Возвращаемся к замене
x² - 2x = -1
x² - 2x + 1 = 0
(x - 1)² = 0
x=1
x² - 2x = 3
x² - 2x - 3 = 0
x=-1
x=3
ответ: ±1; 3
(x² - 2x)² -2(x - 1)² - 1 = 0
(x² - 2x)² - 2(x² - 2x + 1) - 1 = 0
Пусть x² - 2x = t, тогда получаем
t² - 2(t + 1) - 1 = 0
t² - 2t - 3 = 0
По т. Виета:
t1 = -1
t2 = 3
Возвращаемся к замене
x² - 2x = -1
x² - 2x + 1 = 0
(x - 1)² = 0
x=1
x² - 2x = 3
x² - 2x - 3 = 0
x=-1
x=3
ответ: ±1; 3