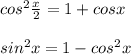
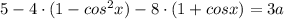
Получаем квадратное уравнение относительно
cosx=t
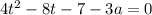
Это уравнение имеет хотя бы один корень, если D ≥0
D=64+16(7+3a)=16(11+3a)
D≥0⇒ 11+3a≥0⇒ a≥ -11/3
t₁=1- (√(11+3а))/2 или t₂=1+ (√(11+3а))/2
Обратная замена приводит к уравнениям вида cos=t₁ или cosx=t₂
Чтобы эти уравнения имели хотя бы один корень, необходимо, что бы
-1 ≤ t₁ ≤1 или -1 ≤ t₂ ≤1
Решаем неравенства:
-1 ≤1+ (√(11+3а))/2 ≤1
-2≤√(11+3а))/2≤0
-4≤√(11+3а)≤0
Решением неравенства является
11+3a=0
a=-11/3
t₁=t₂=1/2
cosx=1/2
x=±(π/3)+2πn, n∈Z
Неравенство
-1 ≤1- (√(11+3а))/2 ≤1
также приводит к ответу a=-11/3
О т в е т. При а=-11/3
x=±(π/3)+2πn, n∈Z
Функция y = x + 4/3 является линейной, т.к. здесь х в первой степени. Эта функция в общем виде может быть представлена как y = ax + b, где a и b - любые числа ( в нашем случае a = 1, а b = 4/3).
Функция y = x (x + 2) / x может быть преобразована в линейную только при условии, что x не равен 0 (при этом условии можно правую часть выражения сократить на х и получить y = x + 2), но в т.к. функция задана общем виде, без этого ограничения, то она не является линейной. Две последние функции содержат х в отрицательной степени (степень х равна -1), они обе не являются линейными.
б)2х²( 1+2х^4)
2.5х-15=14-(14+4х)
5х-15=14-14-4х
5х+4х=15
9х=15
х=15/9
х=1 2/3
4.6а^2-6ax+6ac+6ax+6x^2-6xc-6ac+6xc+6c^2=6a^2+6x^2+6c^2
3.Пусть х кг- яблок в 1-ой корзине
тогда (х+12) кг- во 2-ой корзине
2х кг- в 3-ей корзине
уравнение:
х+ (х+12)+ 2х=56
х+х+12+2х=56
4х=44
х=11(кг)- в 1-ой корзине
1) 11+12= 23(кг)- во 2-ой корзине
2)2 * 11=22(кг)- в 3-ей корзине