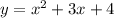
Найдем уравнение касательной, проходящей через точку с абсциссой 
Для этого найдем производную данной функции:
Найдем значение функции в точке с абсциссой :
Найдем значение производной данной функции в точке с абсциссой :
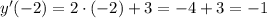
Уравнение касательной имеет вид:
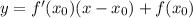
Подставим значение 
Итак, уравнение касательной заданной функции: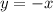 
Воспользуемся геометрическим смыслом касательной: коэффициент наклона 
касательной 
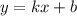численно равен тангенсу угла наклона 
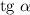с положительным направлением оси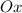 
В найденной касательной коэффициент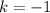 
, следовательно, 
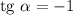при 
или 
ответ: или
Sn=[(n+1)^2]*[n/2]-2n-4n+4-6n+12-8n+24+...-n^2+const+...-4n+4-2n= (1)
=(n^3)/2+n^2+n/2-2n(1+2+3+4+...+n/2)+A(n^2) (2)
<<<Пояснение: представили сумму посл-ти числ-ля как n/2 квадратов сумм пар крайних членов т.е. [(n+1)^2+(n-1+2)^2+(n-2+3)^2+...+([n-n/2]+n/2)^2] и прибавили разницу т.е. напр. для номера 3: (3^2+(n-2)^2)-(3+n-2)^2=-6n+12; для номера 2: -4n+4 и т.д.
Таким образом получили (1)
Далее (2): А(n^2)-величина порядка не более n^2, получаемая при сложении всех свободных членов из (1)>>>
(n^3)/2+n^2+n/2-2n(1+2+3+4+...+n/2)+A(n^2)=(n^3)/2+n^2+n/2-2n([n/2+1]/2*(n/2))+A(n^2)=(n^3)/4+A(n^2)+A(n)+const
Отсюда искомый предел: lim[(n^3)/4+A(n^2)+A(n)+const]/[n^3+3n^2+2] при n->& равен 1/4