
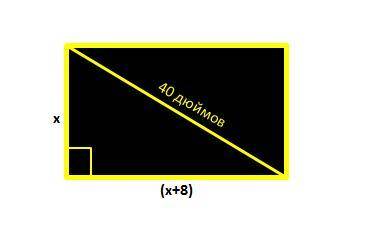
1) Найдем все данные относительно телевизора из условия задачи мы знаем, что телевизор имеет форму прямоугольника (так как "длина экрана телевизора на 8 дюймов больше ширины"), и то что диагональ = 40 дюймов, она является гипотенузой прямоугольного треугольника, ширину возьмем за х, длину за (х+8) (смотрите рисунок)
По теореме Пифагора
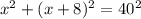
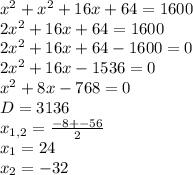
-32 не подходит
Значит ширина 24 дюйма, длина 24+8=32 дюйма
Переведём
24 дюйма = 60,96 см = 0,6096 м
32 дюйма = 81,28 см = 0,8128 м
ответ: Ширина 0,6096 м, длина 0,8128 м
2) Поместится ли такой телевизор в мебельную стенку?
Размеры ниши под телевизор в его мебельной стенке равны 1,2 x 0,8 м.
Длина 1,2 м и ширина 0,8 м, тогда телевизор влезет, так как 0,6096<0,8 и 0,8128<1,2
ответ: Да
Даны координаты параллелограмма: А(1; -2; 3), В(3; 2; 1), D(6; 4; 4).
1) Так как сторона DС параллельна и равна АВ, то приращения координат по осям "x", "у" и "z" у них равны.
АВ: Δx = 3-1 = 2, Δу = 2-(-2) = 4, Δz = 1-3 = -2.
Отсюда х(С) = x(D) + Δx = 6+2 = 8,
у(С) = у(D) + Δу = 4 + 4 = 8.
z(C) = z(D) + Δz = 4 - 2 = 2.
ответ: С(8; 8; 2).
2) АВ = (2; 4; -2).
|AB| = √(4 + 16 + 4) = √24 = 2√6.
AD = (6-1; 4-(-2); 4-3) = (5; 6; 1).
|AD| = √(25 + 36 + 1) = √62.
3) cos A = (2*5 + 4*6 + (-2)*1)/(2√6*√62) = 32/(4√93) = 8√93/93 = 0,829561356.
4) S(ABCD) = AB*AD*sin A = 2√6*√62*0,558415577 = 21,54065922.