Два мальчика стартовали по беговой дорожке длиной 50 метров с интервалом 1 секунда. мальчик, стартовавший вторым, догнал первого в 10 метрах от линии старта , добежал до конца дорожки и побежал обратно с той же скоростью. на каком расстоянии от конца дорожки он встретил первого мальчика , если известно, что эта встреча произошла через 10 секунд после старта первого мальчика?

👇

Ответ:

adiletmurataliev

12.05.2022

Первая встреча(обгон)произошла в 10м от старта.
х с - время движения до первой встречи 1 мальчика
(х-1) с - время до первой встречи 2 мальчика
V=S:t
10/х (м/с) - скорость 1 мальчика
10/(х-1) м/с - скорость 2 мальчика
10с до второй встречи бежал 1 мальчик
10-1=9(с) - время до второй встречи 2 мальчика
Вместе оба мальчика пробежали:
50*2=100м (1 не добежал до 50м, 2-й - пробежал больше 50м)
10/х*10+10/(х-1)*9=100
100/х+90/(х-1)=100, общий знаменатель х(х-1)
100х-100+90х=100х²-100х
100х²-290х+100=0
10х²-29х+10=0
D=b²-4ac
D=841-400=441
х=(29+21)/20
х=2,5(с) - время до первой встречи 1мальчика
10/2,5*10=40(м) - пробежал 1 мальчик до второй встречи
50-40=10(м) - от финиша произошла встреча

4,7(68 оценок)

Открыть все ответы

Ответ:

ALEXAND2033

12.05.2022

3. Прямоугольность треугольника проверяется по формуле

c²=a²+b² (c>b>a)

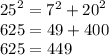
${25}^{2} = {7}^{2} + {20}^{2} \\ 625 = 49 + 400 \\ 625 = 449$

Так как 625≠449, ΔKMP не прямоугольный

6. Высота равнобедренного треугольника находится по формуле

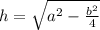
$h = \sqrt{ {a}^{2} - \frac{ {b}^{2} }{4} }$

где h — высота, a — боковая сторона, b — основание

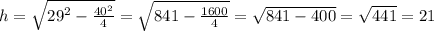
$h = \sqrt{ {29}^{2} - \frac{ {40}^{2} }{4} } = \sqrt{841 - \frac{1600}{4} } = \sqrt{841 - 400} = \sqrt{441} = 21$

высота треугольника равна 21 см

9. По теореме Пифагора (теорема Пифагора гласит, что сумма квадратов катетов равна квадрату гипотенузы): c²=a²+b²

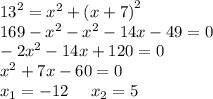
${13}^{2} = {x}^{2} + {(x + 7)}^{2} \\ 169 - {x}^{2} - {x}^{2} - 14x - 49 = 0\\ - 2 {x}^{2} - 14x + 120 = 0 \\ {x}^{2} + 7x - 60 = 0 \\ x_{1} = - 12 \: \: \: \: \: \: x_{2} = 5$

Так как длина не может быть отрицательной a=5, b=5+7=12

Площадь прямоугольного треугольника находится по формуле:

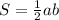
$S = \frac{1}{2} ab$

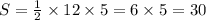
$S = \frac{1}{2} \times 12 \times 5 = 6 \times 5 = 30$

Площадь треугольника равен 30 см²

4,4(46 оценок)

Ответ:

oreo228123

12.05.2022

садовый участок прямоугольной формы площадью 600м квадратных обнесен забором , длина которого 100м . чему равеы стороны участка ? чему равны стороны участка такой же площади , если длина забора вокруг него составляет 140 м ?

Примем

периметр (длина забора) первого участка Р1=100 м

периметр (длина забора) второго участка Р2=140 м

длина первого участка - а1

ширина первого участка - в1

длина второго участка - а2

ширина второго участка - в2

Тогда

(а1+в1)*2=100

(а2*+в2)*2=140

а1*в1=а2*в2=600

а1+в1=50