Есть два метода решения данного уравнения: методом подстановки и методом исключения неизвестных.Я покажу их обоих.
ПодстановкаРешаем уравнение относительно x:
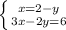
Поставить данное значение x в уравнение 3x-2y=6:
3(2-y)-2y=6
Решаем уравнение относительно y:
6-3y-2y=6
-3y-2y=0
-5y=0
y=0
Подставить данное значение y в уравнение x=2-y:
x=2-0
Решаем уравнение относительно x:
x=2
Решением системы является упорядоченная пара чисел (x,y):
(x,y)=(2,0)
Проверка:
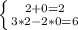
Упростить уравнения:

Упорядоченная пара числе является решением системы уравнений, т.к оба равенства верны:
(x,y)=(2,0)
ИсключениеУмножить обе части уравнения на -3:

Сложить уравнения для исключения по меньшей мере одной неизвестной:
-5y=0
Разделить обе стороны уравнения на -5:
y=0
Подставить данное значение y в простейшее уравнение x+y=2:
x+0=2
Решаем уравнение относительно x:
x=2
Дальше как в предыдущем примере
6. ㏒₂(㏒₃(2.25*4))=㏒₂(㏒₃3²)=㏒₂2=1
7. ㏒₉(tg(270°-30°))=㏒₉(Ctg(30°)=㏒₃²(√3))=㏒₃²(3)¹/²=1/4=0.25
8. 3*(1/2)=1.5; ㏒ₐb³=3㏒ₐb=3/(㏒а по основанию b)
9. упростим числитель 2 ㏒²₃2-(㏒₃3²+㏒₃2)²-㏒₃2*(㏒₃2+2㏒₃)=
2㏒₃²2-4-4㏒₃2-㏒₃²2-㏒₃²2-2㏒₃2=-4-6㏒₃2=-2(2+3㏒₃2), упростим знаменатель. 2㏒₃2+2㏒₃3+㏒₃2=(2+3㏒₃2), после сокращения дроби получим -2(2+3㏒₃2)/(2+3㏒₃2),=-2
10. Упростим первую скобку. (6^(㏒₆5))²=5²=25; 10/10^(lg2)=10/2=5
3^(㏒₃²6²)=6, первая скобка примет вид 25+5-6=24;
Вторая скобка : упростим показатель. (-3㏒₃2-1)/㏒₃2=-3-1/㏒₃2
2^(-3-1/㏒₃2)=(1/8)*1/(2^(1/㏒₃2)=(1/8)*1/(2^(㏒₂3)=1/24
24*(1/24)=1