Дано:
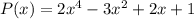
Найти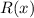 
- остаток от деления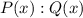 
Решение.
1) Для начала разложим многочлен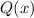 
на множители, для этого решим уравнение:
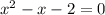
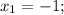
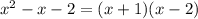
2) Так как данный многочлен 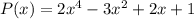делится на 
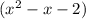с остатком, то представим его в виде
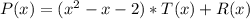
где
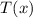- неполное частное;
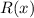- искомый остаток.
Степень остатка деления многочлена на многочлен должна быть меньше степени делителя. В данном случае делитель - многочлен второй степени, так что остаток - многочлен первой степени, который имеет вид:
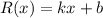
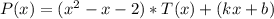
3) Подставим в равенство 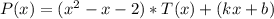первый корень 
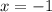и получим:
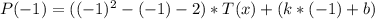
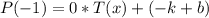
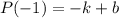
Вычислим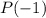 
.
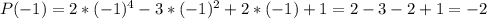
Так как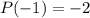 
, то
=> 
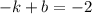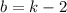
4) Аналогично решаем и со вторым корнем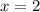 
.
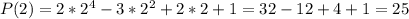
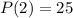
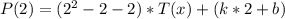
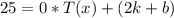
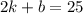
5) Подставим 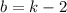в полученное уравнение:
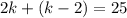
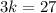
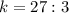
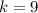
6) 
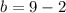
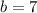
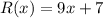- искомый остаток.
ответ: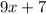 
![\sqrt[3]{b^3} =b](/tpl/images/1360/0500/b0499.png)
- корень нечетной степени
![\sqrt[6]{b^6} =|b|](/tpl/images/1360/0500/b8ca9.png)
- для корней четной степени появляется модуль
Неравенства сводятся к таким: 
и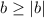 
По определению модуля: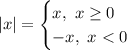 
Таким образом, первое неравенство выполняется всегда. Для положительных чисел и нуля модуль равен самому числу. Для отрицательных чисел, само число меньше модуля, так как модуль будет положительным числом.
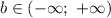
Второе неравенство выполняется при неотрицательных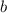 
. Для положительных чисел и нуля модуль по-прежнему равен самому числу. Однако, отрицательное число не может быть больше или равно модуля, так как модуль отрицательного числа - положителен.
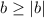
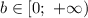
t^2+2t-35=0
D=4+140=144
t12=(-2+-12)/2=-7 5
t=-7
t=7