1) а1=-2 , d=3 , an=118-?
an=a1+(n-1)d
118= -2+(n-1)3
118= -2+3n-3
118 +5=3n
3n=123
n=41
a41=a1+40d= -2 + 120= 118 - является 41 членом арифметической прогрессии.
2) а39=83 ,d= -2 ,a1-?
a39=a1+ 38d
a1= a39 - 38d
a1= 83 - 38•(-2)=83 + 76=159
ответ: а1 = 159
3) а21= - 156, а34= -260, а1-? d-?
a21=a1 +20d --- a1=a21- 20d
a34=a1 +33d --- a1=a34- 33d
a1=a1
a21 -20d=a34 -33d
-20d+33d=a34-a21
13d= -260+156
13d=-104
d=-8
a1=a21-20d= -156-20•(-8)=-156+160= 4
ИЛИ:
а34=а1 + 33d
a34=a21+13d
a34-a21=13d
-260+156=13d
-104=13d
d=-8
a1=a34-33d=-260-33•(-8)=-260+264=4
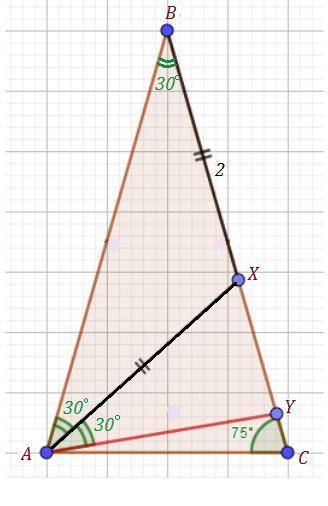
ΔАВС , АВ=ВС , ∠АСВ=75° , точка Х∈ВС , т. Y∈ВС , т. Х∈ВY ,
АХ=ВХ=2 см , ∠ВАХ=∠YАХ . Найти AY .
Так как ΔАВС - равнобедренный и АВ=ВС, то ∠ВАС=∠АСВ=75° ⇒
∠АВС=180°°-75°-75=30°
Так как АХ=ВХ=2 см , то ΔАВХ - равнобедренный и ∠ВАХ=∠АВХ , но ∠АВХ=∠АВС=30° , поэтому ∠ВАХ=30° и ∠АХВ=180°-30°-30°=120° .
Тогда внешний угол ∠AXY=180°-120°=60° .
По условию ∠YAX=∠ВАХ=30° . Тогда в ΔAXY угол ∠AYX=180°-30°-60°=90° , то есть ΔAXY - прямоугольный , в котором гипотенуза АХ=2 см , а катет XY , лежащий против угла в 30°, равен половине гипотенузы, то есть XY=1 cм .
По теореме Пифагора AY²+XY²=AX² ⇒ AY²=AX²-XY²=2²-1²=4-1=3 ,
AY=√3 cм .
все остальные значения известны