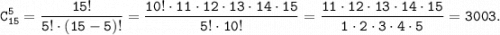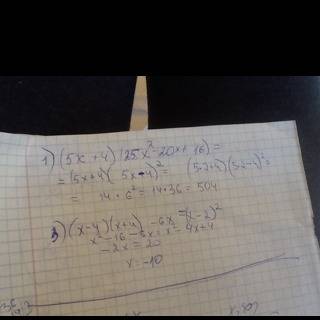
1) Первые 10 простых чисел, от 2 до 29:
2357111317192329
Чтобы получить наибольшее число, нужно вычеркнуть 235 и 111. Получится
7317192329
2) Пусть сумма всех чисел в каждой строке равна а.
Тогда сумма всех чисел в таблице равна М*а.
Сумма чисел в каждом столбце тоже равна а.
Тогда сумма чисел во всей таблице равна К*а.
Но это одно и тоже число.
М*а = К*а
М = К
ЧТД.
3) 1*2+2*3+3*4+4*5+5*6+6*7+7*8+8*9+9*10+...+997*998+998*999+999*1000
Выпишем последние цифры в каждом произведении.
2 + 6 + 2 + 0 + 0 + 2 + 6 + 2 + 0 + 0 +...+ 0 + 0 + 2 + 6 + 2 + 0 =
= (2+6+2) + 0 + (2+6+2) + 0 + ... + 0 + (2+6+2) + 0 = 10 + 0 + 10 + 0 +...+ 10 + 0
Эта сумма оканчивается на 0
4) Нельзя. Количество монет, лежащих орлом вверх, всегда четное.
Сначала 0, потом 20, потом 2 (если я переверну монету, которая осталась решкой вверх, и еще 19, которые стали орлом вверх), и так далее.
Оно не может стать нечетным числом 21.
5) Число 2017 нужно написать 9 раз подряд. Тогда каждая цифра будет повторена 9 раз, и сумма цифр будет делиться на 9, и само число тоже.
Количество цифр в этом числе 4*9 = 36.
6) Сегодня среда. Послезавтра будет пятница.
День, когда "послезавтра" станет "вчера" - это суббота.
День, когда "вчера" было "завтра" - это позавчера, в понедельник.
Понедельник и суббота одинаково далеки от воскресенья - на 1 день.
Объяснение:
Задачу можно решить различными .
. Первого игрока команды можно выбрать среди 15 спортсменов, то есть . Второго игрока команды можно выбрать среди оставшийся 14 спортсменов, то есть . Точно также, третьего игрока команды можно выбрать , четвёртого игрока команды можно выбрать , и наконец, пятого игрока команды можно выбрать .
Однако каждая команда при этом подсчете учтена несколько раз: одна и та же пятёрка спортсменов может быть выбрана по разному, например, сначала А, потом В, потом С, потом D, потом E, или сначала B, потом А, потом C, потом D, потом E и так далее. Поскольку число перестановок из пяти элементов равно 5!=120, то каждая команда учтена нами ровно 120 раз. Поэтому получается, что команду из 5 игроков можно выбрать
.
. Применим формулу комбинаторики.
Определение. Пусть имеется множество, содержащее n элементов. Произвольный неупорядоченный набор, состоящий из k различных элементов данного множества, называется сочетанием из n элементов по k элементов (или просто сочетанием из n по k).
Число сочетаний из n элементов по k элементов обозначается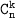 
и вычисляется по формуле:
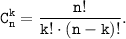
Так как n = 15 и k = 5, то
