Question

Впрямоугольнике авсd со сторонами ав=2, вс=5 случайно выбирают точку. найти вероятность того что она расположена ближе к вершине а, чем к точке пересечения диагоналей. с решением плз

Answer 1

Проведем серединный перпендикуляр к АО. Из прямоугольного треугольника ACD по теореме Пифагора

$AD=\sqrt{2^2+5^2}=\sqrt{29}$

$AK=OK=\frac{1}{2}AO=\frac{1}{4}AC=\frac{\sqrt{29}}{4}$

Треугольники AKM и ACD подобны по двум углам (∠AKM = ∠ADC и ∠А - общий).

AM/AK = AC/AD  ⇒  AM=29/20

Треугольники AKM и NKC подобны по двум углам (∠AKM=∠CKN и ∠KAM = ∠NCK как накрест лежащие при BC || AD и секущей AC).

AM/AK = NC/CK = (BC-BN)/(AC-AK) ⇒ BN = 13/20

Площадь четырехугольника ABNM: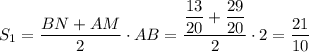 $S_1=\dfrac{BN+AM}{2}\cdot AB=\dfrac{\dfrac{13}{20}+\dfrac{29}{20}}{2}\cdot2=\dfrac{21}{10}$

Площадь прямоугольника ABCD: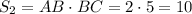 $S_2=AB\cdot BC=2\cdot5=10$

Искомая вероятность по геометрической формуле вероятности:

$P=\dfrac{S_1}{S_2}=\dfrac{\dfrac{21}{10}}{10}=\dfrac{21}{100}=0.21$

ответ: 0,21.