Алгебра: Сократите дробь: 18c^6m^8 27c^3m^9

Сократите дробь: 18c^6m^8 27c^3m^9

👇

Увидеть ответ

Ответ:

Uniquehatter

05.02.2023

Сократите дробь:

18c^6* m^8 /( 27c^3* m^9)=

=2c^3*9c^3*m^8 /( 3*9*c^3* m*8*m)=(сократим одинаковые члены сверху/снизу )

=2c^3 /(3* m)

4,4(36 оценок)

Открыть все ответы

Ответ:

HsbHbaj

05.02.2023

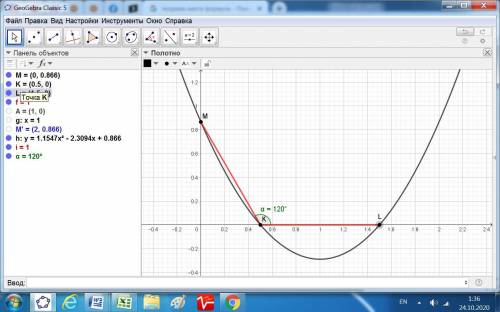
Дан график y = (2/√3)x² + bx + c и условия: KL=KM, ∠LKM=120∘, где L, K и M точки пересечения осей.

Примем координаты корней на оси Ох: х1 и х2.

Координата точки М по у равна коэффициенту с из уравнения.

Из треугольника МОК с учётом угла 180 - 120 = 60 находим соотношение: с = х1*tg60 = x1*√3.

Далее используем равенство KL=KM.

KL=KM = √((х1)² + (x1*√3)²) = √((х1)² + 3(х1)²) = √(4((х1)²) = 2*х1.

Отсюда находим: х2 = х1 + 2х1 = 3х1.

Далее используем теорему Виета для корней.

Для этого надо разделить коэффициенты уравнения на а (2/√3).

Получаем уравнение y = x² +(b/(2/√3))x + c/(2/√3).

Для определения корней правую часть приравняем нулю.

x² +(b/(2/√3))x + c/(2/√3) = 0.

По Виета х1*х2 = c/(2/√3). Заменим с = x1*√3 и х2 = 3х1.

3(х1)² = x1*√3/(2/√3). После сокращения получаем:

х1 = 1/2. Это найден первый корень.

Второй равен 3х1 = 3*(1/2) = 3/2.

ответ: корни равны (1/2) и (3/2).

График квадратного трёхчлена y = 2/√3 * x^2 + bx + c пересекает оси координат в трёх точках K, L и M

4,4(59 оценок)

Ответ:

lolkekpfff

05.02.2023

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. глава 5. решение треугольников 5.1. прямоугольный треугольник аксиомы 1.4 и 2.1 позволяли приписывать отрезкам и углам числа, равные их мерам, то есть измерять отрезки и углы. до сих пор не было связи между величинами углов и длинами отрезков. с введением треугольников появляется возможность связать величины градусных мер углов треугольника и длин его сторон. рассмотрим соотношения между сторонами и углами прямоугольного треугольника. 1 рисунок 5.1.1. прямоугольный треугольник. косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. пусть угол (bac) – искомый острый угол. так, например, для угла bac (рис. 5.1.1) теорема 5.1. косинус угла зависит только от градусной меры угла и не зависит от расположения и размеров треугольника. доказательство пусть abc и a1b1c1 – два прямоугольных треугольника с одним и тем же углом при вершинах a и a1, равным α . построим треугольник ab2c2, равный треугольнику a1b1c1, как показано на рис. 5.1.2. это возможно по аксиоме 4.1. так как углы a и a1 равны, то b2 лежит на прямой ab. прямые bc и b2c2 перпендикулярны прямой ac, и по следствию 3.1 они параллельны. по теореме 4.13 2 рисунок 5.1.2. к теореме 5.1. но по построению ac2 = a1c1; ab2 = a1b1, следовательно, что и требовалось доказать. теорема 5.2. теорема пифагора. в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. модель 5.2. доказательство теоремы пифагора. на рисунке 5.1.3 изображен прямоугольный треугольник. bc и ac – его катеты, ab – гипотенуза. по теореме bc2 + ac2 = ab2. доказательство пусть abc – данный прямоугольный треугольник с прямым углом при вершине c. 3 рисунок 5.1.3. к доказательству теоремы пифагора. проведем высоту cd из вершины c. по определению из треугольника acd и из треугольника abc. по теореме 5.1 и, следовательно, . аналогично из δ cdb, из δ acb, и отсюда ab · bd = bc2. складывая полученные равенства и, замечая, что ad + bd = ab, получаем ac2 + bc2 = ab · ad + ab · bd = ab (ad + bd) = ab2. теорема доказана. в прямоугольном треугольнике любой из катетов меньше гипотенузы. косинус любого острого угла меньше единицы. пусть [bc] – перпендикуляр, опущенный из точки b на прямую a, и a – любая точка этой прямой, отличная от c. отрезок ab называется наклонной, проведенной из точки b к прямой a. точка c называется основанием наклонной. отрезок ac называется проекцией наклонной. с теоремы пифагора можно показать, что если к прямой из одной точки проведены перпендикуляр и наклонные, то любая наклонная больше перпендикуляра, равные наклонные имеют равные проекции, из двух наклонных больше та, у которой проекция больше. синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. по определению тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему. для угла (bac) прямоугольного треугольника, изображенного на рис. 5.1.1, имеем так же как и косинус, синус угла и тангенс угла зависят только от величины угла. 4 рисунок 5.1.4. из данных определений получаем следующие соотношения между углами и сторонами прямоугольного треугольника: если α – острый угол прямоугольного треугольника, то катет, противолежащий углу α , равен произведению гипотенузы на sin α; катет, прилежащий к углу α , равен произведению гипотенузы на cos α; катет, противолежащий углу α , равен произведению второго катета на tg α.

4,5(96 оценок)

Это интересно:

Семейная-жизнь

19.04.2021

Как помочь другу, потерявшему близкого человека: советы и рекомендации...

Здоровье

04.01.2023

Контроль гнева: как управлять своими эмоциями...

Кулинария-и-гостеприимство

02.02.2020

Как сделать красивые и вкусные французские макароны с миндалем...

Кулинария-и-гостеприимство