Объяснение: ЗАДАНИЕ 9 и рисунок к задаче 10 внизу на фото
ЗАДАНИЕ 10
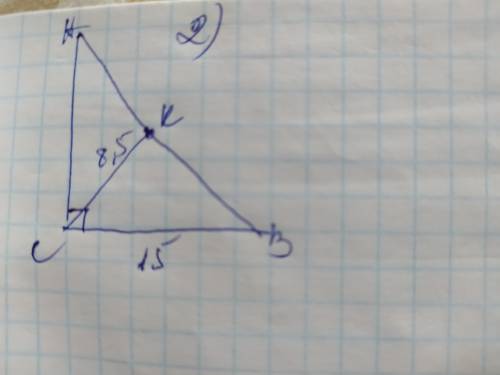
Обозначим вершины треугольника А В С с прямым углом С, катетами АС и ВС и гипотенузой АВ и медианой СК. Если медиана проведена к гипотенузе, то она проведена из прямого угла, а медиана проведённая из вершины прямого угла равна половине гипотенузы, поэтому гипотенуза АВ будет в 2 раза больше медианы: АВ=СК×2=8,5×2=17см
Пусть катет 15см будет катет ВС тогда катет АС найдём по теореме Пифагора:
АС²=АВ²-ВС²=17²-15²=289-225=64;
АС=√64=8см
Площадь треугольника найдём по формуле: S=½×AC×BC=½×15×8=60см²
ОТВЕТ: S=60см²
ЗАДАНИЕ 11
√(49-14а+а²)=√((7-а)²)=7-а
ОТВЕТ: 7-а
ЗАДАНИЕ 12
Если а=5, то: 7-а=7-5=2
ОТВЕТ: 2

ответ: 1004 нуля, 4000 троек, 4001 единица.
Найдём число цифр 3.
Для этого удобно применить метод индукции. Пусть во всех числах От 1 до 10^k-1 , то есть k значное, есть x цифр 3. Найдём сколько цифр 3 находится во всех числах до 10^(k+1)-1 (k+1 значное) . Поскольку у нас есть всего 10(k+1)-ых (0-9) разрядов, а один из этих разрядов соответствует цифре 3, то общее число троек равно : 10*x +10^(k+1)
Среди чисел от 0 до 9 только одна тройка. Тогда общее число троек от 0 до 99 :10*1 +10=20. От 0 до 999 : 10*20+10^2=300 .
От 0 до 9999 : 10*300 +1000=4000.
Таким образом от 1 до 10000 : 4000 цифр 3. Для цифры 1 тот же самый принцип, что и с цифрой 3, только учитываем число 10000 , таким образом : 4001 единица. Для нулей все немного сложнее. Нужно учитывать нули при пустых разрядах. Например : 4029. При учете этих нулей можно легко ошибиться. Но я предлагаю использовать интересную обходную дорогу. Всего в числах от 0 до 9999: 4000 цифр : 1,2,3...9 . Это понятно из вышеуказанного алгоритма. А теперь посчитаем сколько всего в числах от 0 до 9999 вообще всех цифр! Всего 10 однозначных, 90 двузначных , 900 трехзначных и 9000 четырехзначных. Таким образом общее число цифр :10 +90*2 +900*3 +9000*4 =38890
Таким образом цифру 0 написали :
38890 - 4000*9 = 2890
В числах от 1 до 10000 : 2893