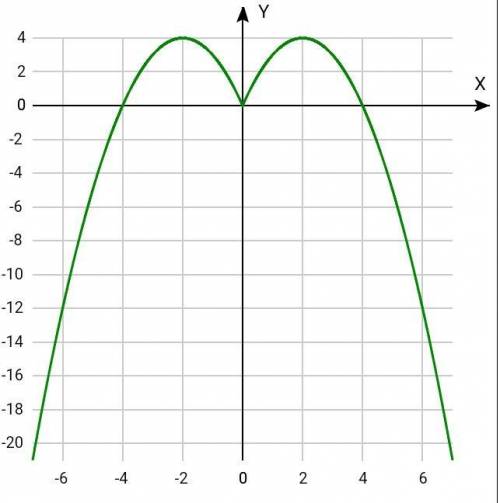
f(x) = 4|x| - x²
1. D(f) = R - симметрична относительно 0.
2. f(-x) = 4|-x| - (-x)² = 4|x| - x² = = f(x),
по определению f(x) - чётнвя.
График чётной функции симметричен относительно оси Оу.
3. Построим часть графика для х ≥ 0, а затем отобразим построенную часть симметрично относительно оси Оу.
f(x) = 4x - x² - квадратичная, графиком является парабола, ветви направлены вниз, т.к. а = - 1, а<0.
х вершины = - b/(2a) = -4/(-2) = 2;
у вершины = 4•2 - 2² = 4;
(2;4) - вершина параболы.
Найдём нули функции:
4x - x² = 0
- х (х - 4) = 0
х = 0 или х = 4
(0;0) и (4;0) - точки пересечения с осью Ох.
Изображение графика смотрите в прикреплённом чертеже.
y=x^2-2 1)Подставим 2-е уравнение в 1-е вместо у. Получим -х-2=x^2-2
y=-x-2. 2) Решим полученное уравнение: -х-2=x^2-2
-x - x^2 = -2+2
x+x^2=0
x(1+x)=0
x=0 1+x=0
x=-1.
3) Найдём у при х =0 и х = -1подставив во 2-е урвнение системы:
При х=0, у = -0-2=-2 (0; -2)
При х = -1, у= -(-1) - 2 = 1 - 2 = -1 (-1;-1)
ответ: (0;-2), (-1;-1)
Сначала возводишь корни в квадрат,тогда мы избавляемся от корней.Получим:
2x^-5x+1=x^2-2x-1;
x^2-3x+2=0;
D=1;
x1=2;
x2=1.
ответ:2,1.