1) 7x - 11 >= 10x - 8
7x - 10x >= 11 - 8
-3x >= 3
x <= -1
2) x^2 - 5x - 36 < 0
D = 5^2 - 4*1(-36) = 25 + 144 = 169 = 13^2
x1 = (5 - 13)/2 = -8/2 = -4; x2 = (5 + 13)/2 = 18/2 = 9
x ∈ (-4; 9)
3) |x + 2| > 3
x + 2 < -3; x < -5
x + 2 > 3; x > 1
x ∈ (-oo; -5) U (1; +oo)
4) 3x^2 - 2x + 1 < 0
D = 2^2 - 4*3*1 = 4 - 12 = -8 < 0
Действительных решений нет.
1) После раскрытия скобок выражение принимает вид:
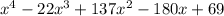 .
.
Эта функция имеет 2 минимума:
1. (0,8; 1,8)
2. (10,2; -36).
2) Запишем пропорцию - a/b = c/d a = b + 6 c = d + 5
(b + 6) / b = (d + 5) / d Отсюда 6d = 5b d = 5b / 6
По условию a^2 + b^2 + c^2 + d^2 = 793
Подставив значения, получим - (b + 6)^2 + b^2 + (d + 5)^2 + d^2 = 793.
После раскрытия скобок - 2b^2 + 12b + 2d^2 + 10d + 61 = 793/
Заменив d = 5b / 6 и приведя к общему знаменателю, получим
72b^2 + 432b + 50b^2 + 300b = 26352 или 122b^2 + 732b - 26352 = 0
Корни этого уравнения равны -18 и 12. Отрицательное значение отбрасываем - b = 12.
а =12 + 6 = 18 - это первый член пропорции
1) 7х - 11 ≥ 10х - 8,
7х - 10х ≥ - 8 + 11,
-3х ≥ 3,
х ≤ -1,
х ∈(-∞; -1]
2) х² - 5х - 36 < 0
х² - 5х - 36 = (x - 9)(x + 4)
х² - 5х - 36 = 0,
D = (-5)² - 4 · 1 · (-36) = 25 + 144 = 169; √169 = 13
x₁ = (5 + 13)/(2 · 1) = 18/2 = 9
x₂ = (5 - 13)/(2 · 1) = -8/2 = -4
х ∈(-4; 9) - см. рис. в прикрепленном файле
3) |x + 2| > 3
x + 2 < -3 (1) или х + 2 > 3 (2)
(1): x< - 3 - 2, x < -5,
(2): x > 3 - 2, x >1
x ∈(-∞; -5) ∪ (1; +∞)
4) 3x² - 2x + 1 < 0
рассмотрим функцию у = 3x² - 2x + 1. Это квадратичная функция, графиком которой является парабола. Выясним, как расположена эта парабола относительно оси Ох. Для этого решим уравнение
3x² - 2x + 1 = 0:
D = (-2)² - 4 · 3 · 1 = 4 - 12 = -8 < 0.
Значит, данная парабола не имеет точек пересечения с осью Ох и, следовательно, принимает только положительные значения.
Итак, данное неравенство решений не имеет