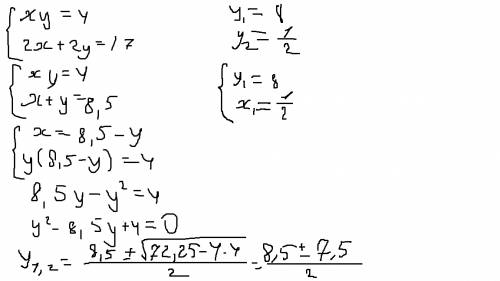
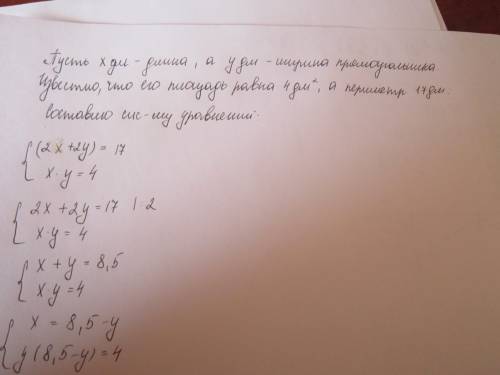
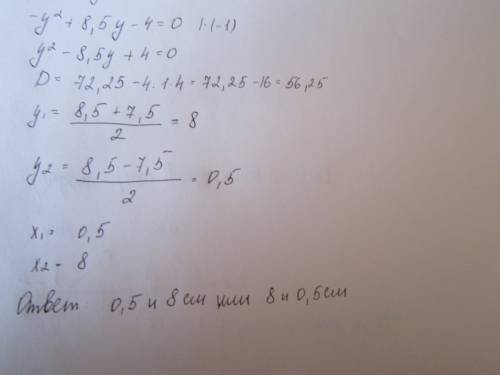
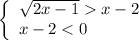
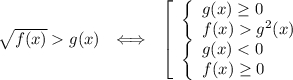
Решаем первое неравенство системы по правилу:
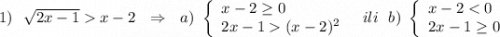
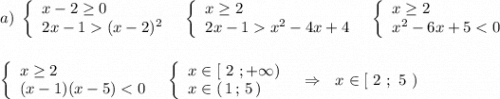
Квадратное неравенство решали методом интервалов:
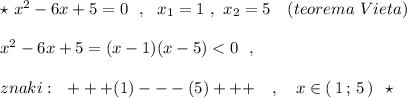
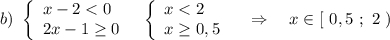
Теперь объединим решения 1 и 2 систем , получим решение 1) иррационального неравенства заданной системы .
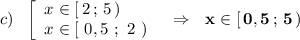
Итак, 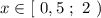 - это решение первого неравенства заданной системы.
- это решение первого неравенства заданной системы.
2) Решаем второе неравенство заданной системы: 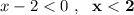 ,
, 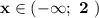 .
.
3) Теперь найдём решение заданной системы как пересечение решений 1-го и 2-го неравенств заданной системы .
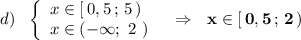
ответ: 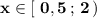 .
.
Можно отметить, что все эти процедуры выполнять не обязательно, так как в условии системы уже задано, что х-2<0 , а (х-2) - это правая часть 1-го неравенства. То есть специально рассматривать случай, когда х-2≥0 не нужно и пункт а) отпадает . Решаем сразу первое неравенство с пункта b) . Как видно по ответу, решением заданной системы является решение системы b) .
Пусть х - скорость велосипедиста, тогда у - скорость пешехода.
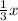 км - расстояние которое за 20 минут велосипедист.
км - расстояние которое за 20 минут велосипедист.
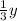 км - расстояние которое за 20 минут пешеход.
км - расстояние которое за 20 минут пешеход.
Зная, что расстояние между пунктами 12 км, составим первое уравнение:
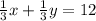 .
.
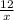 ч - время, которое затратил на дорогу велоепидист.
ч - время, которое затратил на дорогу велоепидист.
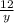 ч - время, которое затратил на дорогу пешеход.
ч - время, которое затратил на дорогу пешеход.
Зная, что пешеход прибыл в пункт А на 1ч 36 мин. позже. чем велосипедист в пункт В, составим второе уравнение:
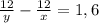 .
.
Составим систему:
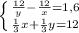
х = 36 - у
12(36 - у) - 12у = 1,6у(36 -у)
y1 = 12
y2 = 90 - не подходит, невозможная скорость дя пешехода
х = 36 - 12 = 24