Произведение меньше 0 только если один из множителей отрицательное число. При -7<х<0 скобка будет положительной, а х - отрицательным, что нам и требуется. Так как неравенство строгое (неменьше или равно, а только меньше), то х не может быть равен 0 или -7.
ответ: -7<х<0
Объяснение:
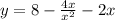
На 0 делить нельзя. Область определения: (-∞;0)∪(0;∞)
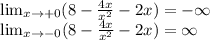
Т.к х не равен 0, то точек пересечения с осью у нет. Находим точки пересечения с осью х.
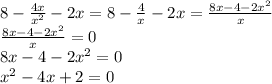
Решаем квадратное уравнение, находим точки пересечения с осью х:
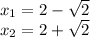
Находим точки экстремума (производная равна нулю).
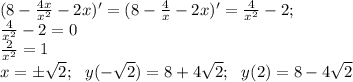
Для нахождения точек перегиба находим вторую производную
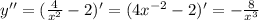
Вторая производная нигде не равна нулю, точек перегиба нет.
Горизонтальных асимптот нет. Вертикальная асимптота одна: х=0.
Ищем наклонную асимптоту:
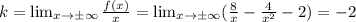
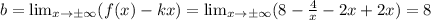
Наклонная асимптота есть:
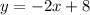
Дальнейшее исследование проводим, заполняя таблицу (см. рис.1).
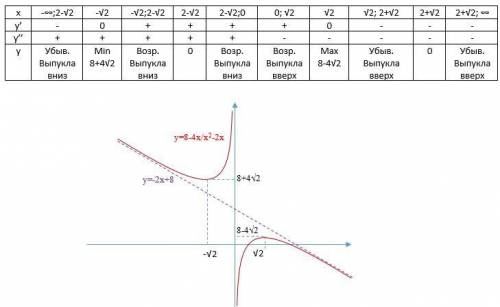
несложно.
х<0
х<-7
х принадлежит промежутку (-7;0)