1.а) y=6*0.5+19=3+19=22 б) 1=6x+19 6x=18 x=3 в) 7=-2*6+19=1 - не проходит. 2.а) проведите прямую через точки 0 и точку а(3; 2) б) y=2*1.5-4=-1 3. y=-2x - возьмите точку x (например 2, тогда y=-4) и проведите горизонтальную прямую на координатной плоскости. y=3 - проведите горизонтальную прямую, где значение y=3 4. 47x-37=-13x+23 60x=60 x=1 y=47-37=10 y=-13+23=10 точка пересечения двух графиков функций = а(1; 10) 5. y=3x-7 пусть x=2 и x=3, тогда y=-1 и y=2 a(2; -1) b(3; 2) тогда пусть параллельный график будет с точками o(0; 0) и c(1; 3) тогда y=3x - искомая формула линейной функции
Касательная - это такая прямая, которая касается графика функции в какой-либо точке, и нигде не пересекая. Функция f(x) = 2x^2 -6x + 1 представляет собой параболу, ветви которой направлены вверх (коэффициент перед x^2 больше нуля). Представили параболу? Нарисуйте её. У параболы только касательная в её вершине параллельна оси Ох. Абсцисса вершины ищется по формуле (должны знать её) x0 = - b/(2a) = - (-6)/(2*2) = 6/4 = 3/2 Для нахождения ординаты (координаты y), значение х0 подставляем в формулу функции. y0 = f(3/2) =-3.5 Точка, где касательная параллельна оси Ох, единственная, её координаты: x =1.5; y = -3.5
1. x-3y=2
х=3у+2
2. у(3y+2)+y=6
3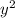
+3y-6=0
y1=1; y2=-3
3. Если у1=1,то х=5
Если у2=-3,то х=-7
ответ: