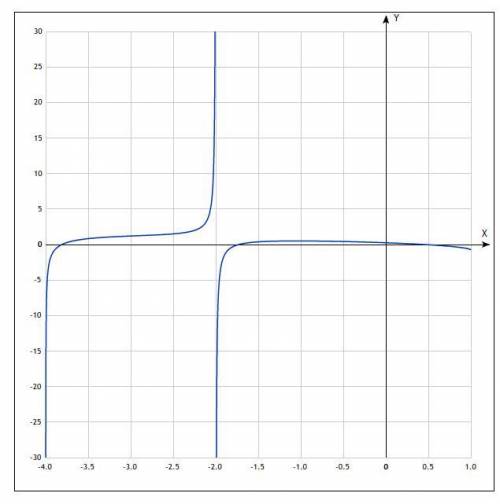
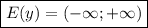Алгебра: Выражения (12-d)(12+d) (4n-7m)(4n+7m) (3a-b^2)(b^2 +3a)

Функция, конечно, интересная, но искать производную или просто нули функции, очень сложно. Будем рассматривать критические точки функции и искать пределы.1. Найдем область определения функции:Здесь же видно, какие пределы надо считать. Посчитаем предел справа для (это всякие -3.9999 и т.д.)Очевидно, что рассматривать всегда надо одно слагаемое, которое приводит знаменатель в 0.То есть слева график уходит в минус бесконечность, для области значений делаем выводы.Теперь дальше, после (-4) следующая...

Выражения (12-d)(12+d) (4n-7m)(4n+7m) (3a-b^2)(b^2 +3a)

👇

Увидеть ответ

Ответ:

gilkatay1

22.03.2023

поблагодари))

4,5(23 оценок)

Открыть все ответы

Ответ:

Яприсоединилась

22.03.2023

Объяснение: 1) ∫₄⁹√xdx =(2/3)·x√x |₄⁹= (2/3)· (9√9 = 4√4)=(2/3)·(27-8)= 2·19/3=38/3

2) 1+ log₂(x+5) = log₂(3x-1) +log₂(x-1) , ОДЗ: х-1>0, x>1 ⇔ log₂2 +log₂(x+5) = log₂(3x-1) +log₂(x-1) ⇔ log₂ (2x+10) = log₂ (3x²-4x+1) ⇒ 2x+10= 3x²-4x+1 ⇒ 3x²-6x-9 =0⇒ x²-2x - 3=0, D= 4+12=16>0, ⇒x₁=(2+4)/2=3, x₂=(2-4)/2=-1 (не удовлетворяет ОДЗ уравнения). ответ: х=3 №3 tgα=y'(x₀), y'(x)=(x³)'=3x² ⇒ т.к. х₀ =0, то tgα=y'(x₀)=3·0²=0

4,5(73 оценок)

Ответ:

alexalevdorovic

22.03.2023

Функция, конечно, интересная, но искать производную или просто нули функции, очень сложно. Будем рассматривать критические точки функции и искать пределы.

1. Найдем область определения функции:

$\left\{\begin{matrix} 1-x\geq0\\ x+4 0\\ x^2-4 \neq 0\end{matrix}\right. \Rightarrow \left\{\begin{matrix} x \leq 1\\ x -4\\ x \neq \pm2\end{matrix}\right.\Rightarrow x\in(-4;-2)\cup(-2;1]$

Здесь же видно, какие пределы надо считать. Посчитаем предел справа для 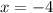x=-4 (это всякие -3.9999 и т.д.)

Очевидно, что рассматривать всегда надо одно слагаемое, которое приводит знаменатель в 0.

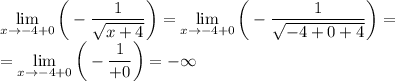
$\displaystyle \lim_{x\to-4+0}\bigg(-\frac{1}{\sqrt{x+4}}\bigg)=\lim_{x\to-4+0}\bigg(-\frac{1}{\sqrt{-4+0+4}}\bigg)=\\=\lim_{x\to-4+0}\bigg(-\frac{1}{+0}\bigg)=-\infty$

То есть слева график уходит в минус бесконечность, для области значений делаем выводы.

Теперь дальше, после (-4) следующая интересная точка (-2), рассмотрим предел слева для неё.

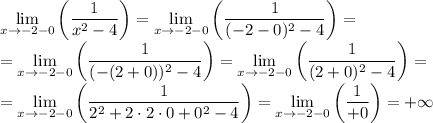
$\displaystyle \lim_{x\to-2-0}\bigg(\frac{1}{x^2-4}\bigg)=\lim_{x\to-2-0}\bigg(\frac{1}{(-2-0)^2-4}\bigg)=\\=\lim_{x\to-2-0}\bigg(\frac{1}{(-(2+0))^2-4}\bigg)=\lim_{x\to-2-0}\bigg(\frac{1}{(2+0)^2-4}\bigg)=\\=\lim_{x\to-2-0}\bigg(\frac{1}{2^2+2\cdot 2\cdot 0+0^2-4}\bigg)=\lim_{x\to-2-0}\bigg(\frac{1}{+0}\bigg)=+\infty$

То есть на интервале 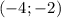(-4;-2) функция уже принимает значения 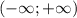$(-\infty; +\infty)$ . Этого уже достаточно, чтобы ответить на вопрос задачи, потому что разрывов внутри интервала нет, а значит, функция обязательно достигнет каждого заявленного значения, ведь на этом интервале она непрерывна.

Но ради интереса посмотрим предел справа

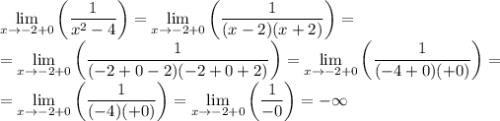
$\displaystyle \lim_{x\to-2+0}\bigg(\frac{1}{x^2-4}\bigg)=\lim_{x\to-2+0}\bigg(\frac{1}{(x-2)(x+2)}\bigg)=\\=\lim_{x\to-2+0}\bigg(\frac{1}{(-2+0-2)(-2+0+2)}\bigg)=\lim_{x\to-2+0}\bigg(\frac{1}{(-4+0)(+0)}\bigg)=\\=\lim_{x\to-2+0}\bigg(\frac{1}{(-4)(+0)}\bigg)=\lim_{x\to-2+0}\bigg(\frac{1}{-0}\bigg)=-\infty$

То есть при переходе через точку x=-2 функция с положительной бесконечности прыгает на отрицательную, в целом это нормально для гипербол.

И последний предел, который посчитаем, это при 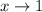$x\to1$ , просто это правый конец области определения.

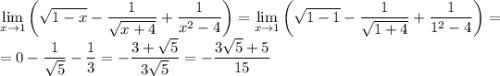
$\displaystyle\lim_{x\to1}\bigg( \sqrt{1-x}-\frac{1}{\sqrt{x+4}}+\frac{1}{x^2-4} \bigg)=\lim_{x\to1}\bigg( \sqrt{1-1}-\frac{1}{\sqrt{1+4}}+\frac{1}{1^2-4} \bigg)=\\=0-\frac{1}{\sqrt{5}}-\frac{1}{3}=-\frac{3+\sqrt{5}}{3\sqrt{5}}=-\frac{3\sqrt{5}+5}{15}$

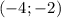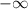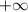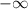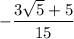
То есть функция на (-4;-2) (имеем в виду -2-0) растет от $-\infty$ до $+\infty$ (необязательно монотонно), затем на (-2;1] (имеем в виду -2+0) растет от $-\infty$ до $\displaystyle -\frac{3\sqrt{5}+5}{15}$