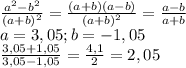
Объяснение:
1.
C⁵ₓ₊₁=(3/8)*A³ₓ
(x+1)!/((x+1-5)!*5!)=(3/8)*x!/(x-3)!
(x+1)!/((x-4)!*5!)=(3/8)*x!/((x-4)!(x-3))
x!*(x+1)/5!=(3/8)*x!/(x-3)
(x+1)/5!=(3/8)/(x-3)
(x-3)*(x+1)=(3/8)*120
x²-2x-3=45
x₂-2x-48=0 D=196 √D=14
x₁=-6 ∉ x₂=8.
ответ: х=8.
2.
Cˣ⁻⁴ₓ₊₁=(7/15)*A³ₓ₊₁
(x+1)!/((x+1-(x-4))!*(x-4)!=(7/15)*(x+1)!/(x+1-3)!
(x+1)!/(5!*(x-4)!=(7/15)*(x+1)!/(x-2)!
1/(5!*(x-4)!)=(7/15)/((x-4)!*(x-3)*(x-2))
1/5!=(7/15)/((x-3)*(x-2))
15*(x-3)*(x-2)=7*5!
15*(x²-5x+6)=7*120 |÷15
x²-5x+6=7*8
x²-5x+6=56
x²-5x-50=0 D=225 √D=15
x₁=-5 ∉ x₂=10.
ответ: х=10.
Я не стану спецом лезть в инет и чекать где она применяется, я лишь приведу свои примеры, где тригонометрия мне пригодилась, да они будут тупыми, но все же :D
Во-первых, без тригонометрии очень сложно в физике, при решении сложных физических задач на механику, электродинамику очень часто приходится знать тригонометрию, особенно в теме колебательного движения, так как гармонические колебания происходят по закону синуса или косинуса, то есть графиком будет синусоида.
Во-вторых, когда тебе может быть скучно, допустим ты находишься в своей машине на горке под определенным углом к горизонту и тебе нужно найти проекцию силы тяжести, которая тянет твою машину вниз, то без тригонометрии тоже сложно это сделать. Ну это все шутки конечно...
Тригонометрия нужна в разработке 3-D игр, даже не зачем объяснять почему - это итак очевидно, нужно, допустим, определить траекторию полета какого-то тела или проверить столкнутся ли тела, либо тебе необходимо заставить объект двигаться в любом направлении - это все без так называемых "синусов" и "косинусов" не сделать.
Вообщем говоря стоит признать уже всем, что без тригонометрии нам никуда и как ни крути все равно придется ее знать.
при a=3.05, b=-1.05: