1) - "Инструкция по построению графика своими руками";
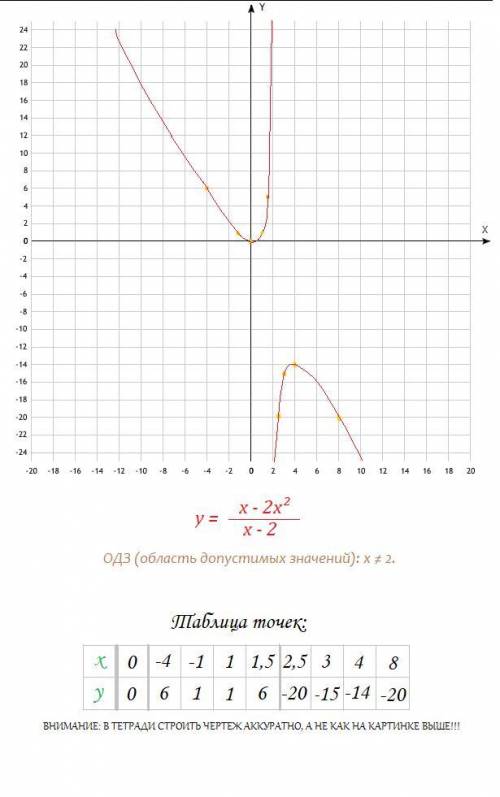
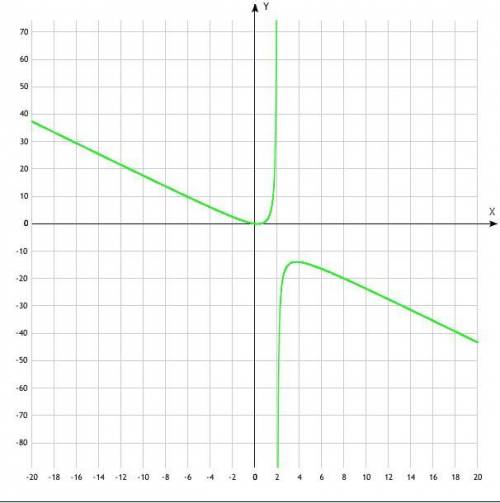
2) - Сам график;
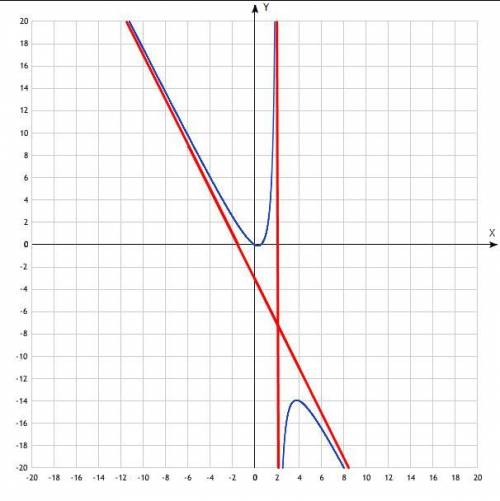
3). - Асимптоты.
_____________________________________
Асимптоты здесь - это вертикальная прямая, параллельная оси ординат и проходящая через точку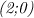 
(задается уравнением 
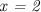) и наклонная, которая, как показывают вычисления, является графиком линейной функции 
.
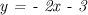Пересечения с осями координат происходят в точках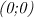 
и 
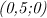. Чтобы их найти, достаточно в уравнение, задающее функцию, поочередно подставить 
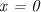и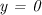 
.
А таблица точек - в прикрепленном файле.
Заметим, что при умножении двух чисел последняя цифра равна последней цифре произведения последних цифр, т.е. если одно число оканчивается на цифру а, а другое - на цифру b, то произведение оканчивается на последнюю цифру ab.
7¹ = 7 - оканчивается на 7
7² = 7×7 = 49 - оканчивается на 9
7³ = 7²×7 - оканчивается на то же, что и 9×7, т. е. 63 - оканчивается на 3
7⁴ = 7³×7 - оканчивается на то же, что и 3×7, т. е. 21 - оканчивается на 1
7⁵ = 7⁴×7 - оканчивается на то же, что и 1×7, т. е. 7 - оканчивается на 7
Процесс повторяется:
7⁶ оканчивается на 9
7⁷ - на 3
7⁸ - на 1
7⁹ - на 7
7¹⁰ - на 9
и т.д.
Если степень делится на 4 (7⁴, 7⁸, 7¹² и т.д.) - число оканчивается на 1
Если при делении на 4 степень даёт остаток 1 (7¹, 7⁵, 7⁹ и т.д.) - число оканчивается на 7
Если даёт остаток 2 (7², 7⁶, 7¹⁰ и т.д.) - на 9
Если остаток 3 (7³, 7⁷, 7¹¹ и т.д.) - на 3
69 при делении на 4 даёт остаток 1 (68=4×17), значит 7⁶⁹ оканчивается на 7. Значит 7⁶⁹+3 оканчивается на 0 - т.е. делится на 10, что и требовалось доказать
x=(-k+-√(k²+48))/8 x1=(-k+√(k²+48))/8 x2=(-k-√(k²+48))/8 подставим
|(-k+√(k²+48))/8+(-k-√(k²+48))/8|=2 |-k/4|=2 k/4=2 k=8
4x^2+8x-3=0