Для начала, нужно разложить числитель и знаменатель на множители. Применим для этого формулу разности кубов для числителя и формулу разности квадратов для знаменателя.
Разность кубов: a^3 - b^3 = (a - b)(a^2 + ab + b^2)
Разность квадратов: a^2 - b^2 = (a - b)(a + b)
Теперь сократим эту дробь. Для этого нужно сократить общие множители в числителе и знаменателе.
Заметим, что оба множителя числителя и знаменателя имеют общий множитель (6a - 1). Поэтому мы можем сократить этот множитель и получить окончательный ответ:
Для решения этой задачи нам понадобится некоторое представление о числах и их свойствах.
1. Вес каждой гири можно представить натуральным числом, так как вес никогда не будет отрицательным или дробным числом.
2. Предположим, что у Васи есть 10 куч с равными весами, тогда в каждой куче будет гирь: 20 / 10 = 2 гири. Пусть первая куча будет самой легкой.
3. Расставим гири по кучам таким образом:
- Первая куча: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20
- Вторая куча: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19
4. Отличие между любыми двумя гирами из первой кучи равно 2, а из второй кучи - 2. Давайте сравним все возможные комбинации гирь из первой кучи с комбинациями гирь из второй кучи:
- Разница между 2 и 1 равна 1. Удвоим это число, получим 2. Заметим, что это не 4.
- Разница между 4 и 1 равна 3. Удвоим это число, получим 6. Заметим, что это не 4.
- Разница между 6 и 1 равна 5. Удвоим это число, получим 10. Заметим, что это не 4.
- Разница между 8 и 1 равна 7. Удвоим это число, получим 14. Заметим, что это не 4.
- Разница между 10 и 1 равна 9. Удвоим это число, получим 18. Заметим, что это не 4.
- Разница между 12 и 1 равна 11. Удвоим это число, получим 22. Заметим, что это не 4.
- Разница между 14 и 1 равна 13. Удвоим это число, получим 26. Заметим, что это не 4.
- Разница между 16 и 1 равна 15. Удвоим это число, получим 30. Заметим, что это не 4.
- Разница между 18 и 1 равна 17. Удвоим это число, получим 34. Заметим, что это не 4.
- Разница между 20 и 1 равна 19. Удвоим это число, получим 38. Заметим, что это не 4.
- Разница между 2 и 3 равна 1. Удвоим это число, получим 2. Заметим, что это не 4.
- Разница между 4 и 3 равна 1. Удвоим это число, получим 2. Заметим, что это не 4.
- Разница между 6 и 3 равна 3. Удвоим это число, получим 6. Заметим, что это не 4.
- Разница между 8 и 3 равна 5. Удвоим это число, получим 10. Заметим, что это не 4.
- Разница между 10 и 3 равна 7. Удвоим это число, получим 14. Заметим, что это не 4.
- Разница между 12 и 3 равна 9. Удвоим это число, получим 18. Заметим, что это не 4.
- Разница между 14 и 3 равна 11. Удвоим это число, получим 22. Заметим, что это не 4.
- Разница между 16 и 3 равна 13. Удвоим это число, получим 26. Заметим, что это не 4.
- Разница между 18 и 3 равна 15. Удвоим это число, получим 30. Заметим, что это не 4.
- Разница между 20 и 3 равна 17. Удвоим это число, получим 34. Заметим, что это не 4.
Похоже, что рассмотрение комбинаций гирь из разных куч не помогло нам найти пару гирь с разницей веса в 4 раза. Однако, необходимо упомянуть, что все рассмотренные гири суммарно покрывают множество чисел от 2 до 39. Обратите внимание, что разница между любыми двумя числами из этого диапазона будет находится в промежутке от 1 до 37.
5. Перепишем гиры из первой и второй кучи в один список с возрастанием их веса:
Все разницы равны 1. В этом списке нет чисел, которые делятся на 4.
Теперь перейдем к разбиению гирь на 11 куч с равными весами. Проведем аналогичные шаги:
1. Предположим, что у Васи есть 11 куч с равными весами, тогда в каждой куче будет гирь меньше, чем в предыдущем случае: 20 / 11 = 1 гиря с остатком 9 гирь.
f (x)=3х3+4x-1
(3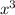
+4x-1)'=3*3
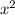+4=9
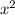+4
x=3
9*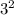
+4=9*9+4=85