Задача: Из A в B одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого авт-ста на 17 км/ч, а вторую половину пути проехал со скоростью 102 км/ч, в результате чего прибыл в В одновременно с первым авт-стом. Найдите скорость первого автомобилиста, если известно, что она больше 65 км/ч.
Обозначим скорость первого автомобилиста за x (км/ч), тогда сорсть второго на первом полупути — ха x−17 (км/ч), на втором полупути — 102 км/ч. Оба проехали общий путь за одно и то же время. Составим и решим уравнение, при условии, что x > 65 (км/ч).
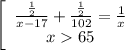
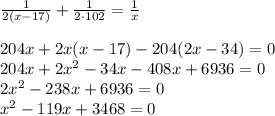
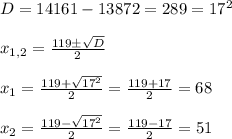
x₂ = 51 < 65 — не удовлетворяет условие
х₁ = 68 > 65 — удовлетворяет условие
ответ: Скорость первого автомобилиста — 68 км/ч.
2 (км/час) - скорость течения реки
Объяснение:
х - скорость течения реки
9+х - скорость лодки по течению
9-х - скорость лодки против течения
77/(9+х) - время лодки по течению
77/(9-х) - время лодки против течения
По условию задачи на путь по течению затрачено на 4 часа меньше, уравнение:
77/(9-х) - 77/(9+х) = 4
Избавляемся от дробного выражения, общий знаменатель (9-х)(9+х) или 81-х², надписываем дополнительные множители над числителями:
77(9+х) - 77(9-х)=4(81-х²)
693+77х-693+77х=324-4х²
4х²+154х-324=0/4 разделим уравнение на 4 для удобства вычислений:
х²+38,5х-81=0
х₁,₂=(-38,5±√1482,25+324)/2
х₁,₂=(-38,5±√1806,25)/2
х₁,₂=(-38,5±42,5)/2
х₁= -81/2= -40,5 отбрасываем, как отрицательный
х₂= 4/2=2 (км/час) - скорость течения реки
Проверка:
77: 11=7 (часов) время по течению
77 : 7=11 (часов) время против течения
11-7=4 (часа) - разница, всё верно.
cos^2t-(ctg^2t + 1) * sin^2 t = cos^2t - 1/sin^2t * sin^2t = cos^2t - 1 = -(1-cos^2t) = -sin^2t