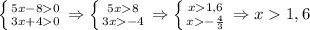
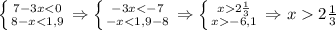
Правильное условие такое:
Мяч брошен вертикально вверх с начальной скоростью 24 м/с. Зависимость расстояния h (в метрах) от мяча до земли от времени полета выражается формулой h = 24t − 5t² .
Дано:
V₀=24м/с
Найти: h; t
1) Скорость - это производная от расстояния.
V = h'
V = ( 24t − 5t²)'
V = 24 - 10t
Получили формулу, которая показывает зависимость скорости V
(в м/с) от времени полета t .
2) V = 24 - 10t
V - конечная скорость, которая в момент достижения мячом наибольшей высоты равна 0.
Решим уравнение и найдем время t.
0 = 24 - 10t
10t = 24
t = 24:10
t = 2,4
t=2,4 с - время полёта мяча снизу до наибольшей высоты.
3) Находим значение наибольшей высоты, на которую поднимется мяч за t=2,4c.
h=24t-5t² при t=2,4c.
h = 24·2,4 - 5·2,4² = 2,4·(24-5·2.4) = 2,4·(24-12) = 2,4·12= 28,8 м
4) Найдем tₓ все время полета от броска с земли до момента падения его на землю
tₓ = 2t = 2 · 2,4 = 4,8c
ответ: 28,8 м; 4,8c
Неравенство имеет 6 целых решений.
Объяснение:
2|x+3| ≤ |x-1|
x+3=0 x-1=0
x=-3 x=1
-3 1
На каждом из промежутков определяем знаки модулей и решаем неравенство:
1) (-∞;-3)
-2(x+3) ≤ -(x-1)
-2x-6 ≤ -x+1
-2x+x ≤ 6+1
-x ≤ 7
x ≥ -7
[-7;-3) - решение на промежутке (-∞;-3)
2) [3;1)
2(x+3) ≤ -(x-1)
2x+6 ≤ -x+1
2x+x ≤ 1-6
3x ≤ -5
x ≤ -5/3
х ≤ -1 ²/₃
[-3; -1 ²/₃] - решение на промежутке [-3;1)
3) [1;+∞)
2(x+3) ≤ x-1
2x+6 ≤ x-1
2x-x ≤ -1-6
x ≤ -7
На промежутке [1;+∞) решений нет
[-7;-3)∪[-3;-1 ²/₃] - множество решений неравенства
{-7;-6;-5;-4;-3;-2} - множество целых решений неравенства.
Всего 6 целых решений неравенства