Формулой log{a^k}b=(1/k)*log{a}b приводиш к общему основанию 2
Нарисуем график функции Y = √ X как повернутую на 90 градусов левую половину параболы Y = X².
1) Проведем горизонтальную прямую Y = 3. Она пересекает данный график при Х = 9
2) Проведем горизонтальную прямую Y = 5. Она пересекает данный график при Х= 25
3) Проведем прямую Y = X (биссектрису прямого угла). Она пересекает график при Х = 0 и Х = 1. Следовательно, уравнение имеет 2 корня.
4) Поскольку функция корня определена при Х ≥ 0, то -Х ≤ 0 и, следовательно решением может быть только Х = 0. Это значение и будет единственным корнем.
Здесь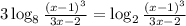
Если дальше будет не решаться, пиши в личку, тогда допишу решение до того места, где застрянешь.